题目内容
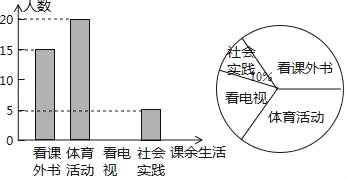
【题目】为了解某中学学生课余生活情况，对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计．现从该校随机抽取n名学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名学生只能选择其中一项）．并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图．由图中提供的信息，解答下列问题：
（1）求n的值；
（2）若该校学生共有1200人，试估计该校喜爱看电视的学生人数；
（3）若调查到喜爱体育活动的4名学生中有3名男生和1名女生，现从这4名学生中任意抽取2名学生，求恰好抽到2名男生的概率．
【答案】（1）n=50；（2）240人；（3）
.
【解析】
（1）用参加社会实践活动的学生人数除以参加社会实践活动的学生人数所占的百分比即可求得n的值；（2）用1200乘以喜爱看电视的学生人数的百分比即可求解；（3）画出树状图，求得所有等可能的结果及恰好抽到2名男生的结果数，利用概率公式求解即可.
解：（1）n=5÷10%=50；
（2）样本中喜爱看电视的人数为50﹣15﹣20﹣5=10（人），
1200×
=240，
所以估计该校喜爱看电视的学生人数为240人；
（3）画树状图为：
共有12种等可能的结果数，其中恰好抽到2名男生的结果数为6，
所以恰好抽到2名男生的概率=
=
．
练习册系列答案
相关题目
