题目内容
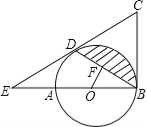
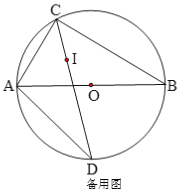
【题目】如图,⊙![]() 是Rt△ABC的外接圆,∠ACB=90°,点I是△ABC的内心,CI的延长线交⊙O于点D,连接AD.
是Rt△ABC的外接圆,∠ACB=90°,点I是△ABC的内心,CI的延长线交⊙O于点D,连接AD.
(1)求证:DA=DI.
(2)若AB=10,AC=6,求AD、CD的长.

【答案】(1)证明见解析;(2)AD=5![]() ;CD=7
;CD=7![]() .
.
【解析】
(1)连接AI,AD,BD,运用圆周角定理、内切圆的性质及三角形外角的性质问题即可求得∠AID=∠DAI,得出DA=DI.
(2)连接![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,由
,由 ![]() 是⊙
是⊙![]() 的直径 ,可得
的直径 ,可得 ![]() °
°
再证△![]() 是等腰直角三角形,在
是等腰直角三角形,在![]() △
△![]() 中和
中和![]() △
△![]() 中,由勾股定理得结果.
中,由勾股定理得结果.
解:(1)证明:连接![]()
∵点![]() 是△
是△![]() 的内心
的内心
∴ ![]() ,
,![]()
∵ ![]()
∴ ![]()
∵ ![]() ,
, ![]()
∴ ![]()
∴ ![]()
(2)连接![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]()
∵ ![]() 是⊙
是⊙![]() 的直径
的直径
∴ ![]() °
°
∵ ![]() °
°
∴ ![]() °
°
∵在![]() △
△![]() 中
中 ![]()
∴ ![]()
∵ ![]()
∴ ![]() °
°
∵在![]() △
△![]() 中
中 ![]() °
°
∴ ![]() °
°
∴ ![]()
∵ 在![]() △
△![]() 中
中 ![]()
∴![]()
∵ 在![]() △
△![]() 中
中 ![]()
∴ ![]()
∴ ![]()
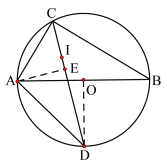
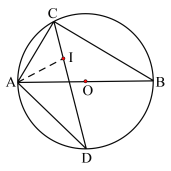
图1 图2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目