ћвƒњƒЏ»Ё
°Њћвƒњ°њ»зЌЉ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђµг![]() ќ™„ш±к‘≠µг£ђ≈„ќпѕя
ќ™„ш±к‘≠µг£ђ≈„ќпѕя![]() љї
љї![]() ÷б”Џ
÷б”Џ![]() £ђ
£ђ![]() Ѕљµг£ђљї
Ѕљµг£ђљї![]() ÷б”Џµг
÷б”Џµг![]() £ђ÷±ѕя
£ђ÷±ѕя![]() Њ≠єэ
Њ≠єэ![]() £ђ
£ђ![]() Ѕљµг£Ѓ
Ѕљµг£Ѓ
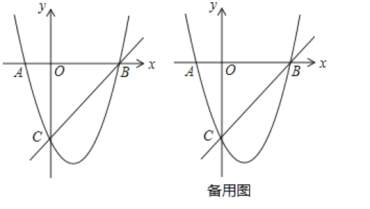
£®1£©«у≈„ќпѕяµƒљвќц љ£ї
£®2£©єэµг![]() „ч÷±ѕя
„ч÷±ѕя![]() ÷бљї≈„ќпѕя”ЏЅн“їµг
÷бљї≈„ќпѕя”ЏЅн“їµг![]() £ђµг
£ђµг![]() «÷±ѕя
«÷±ѕя![]() ѕ¬Јљ≈„ќпѕя…ѕµƒ“їЄцґѓµг£ђ«“‘Џ≈„ќпѕяґ‘≥∆÷бµƒ”“≤а£ђєэµг
ѕ¬Јљ≈„ќпѕя…ѕµƒ“їЄцґѓµг£ђ«“‘Џ≈„ќпѕяґ‘≥∆÷бµƒ”“≤а£ђєэµг![]() „ч
„ч![]() ÷б”Џµг
÷б”Џµг![]() £ђ
£ђ![]() љї
љї![]() ”Џµг
”Џµг![]() £ђљї
£ђљї![]() ”Џµг
”Џµг![]() £ђЅђљ”
£ђЅђљ”![]() £ђєэµг
£ђєэµг![]() „ч
„ч![]() ”Џµг
”Џµг![]() £ђ…иµг
£ђ…иµг![]() µƒЇб„ш±кќ™
µƒЇб„ш±кќ™![]() £ђѕяґќ
£ђѕяґќ![]() µƒ≥§ќ™
µƒ≥§ќ™![]() £ђ«у
£ђ«у![]() ”л
”л![]() ÷ЃЉдµƒЇѓ эљвќц љ£®≤ї“™«у–і≥ц„‘±дЅњ
÷ЃЉдµƒЇѓ эљвќц љ£®≤ї“™«у–і≥ц„‘±дЅњ![]() µƒ»°÷µЈґќІ£©£ї
µƒ»°÷µЈґќІ£©£ї
£®3£©‘Џ£®2£©µƒћхЉюѕ¬£ђЅђљ”![]() £ђєэµг
£ђєэµг![]() „ч
„ч![]() ”Џµг
”Џµг![]() £®µг
£®µг![]() ‘Џѕяґќ
‘Џѕяґќ![]() …ѕ£©£ђ
…ѕ£©£ђ![]() љї
љї![]() ”Џµг
”Џµг![]() £ђЅђљ”
£ђЅђљ”![]() љї
љї![]() ”Џµг
”Џµг![]() £ђµ±
£ђµ±![]() ±£ђ«уѕяґќ
±£ђ«уѕяґќ![]() µƒ≥§£Ѓ
µƒ≥§£Ѓ
°Њір∞Є°њ£®1£©![]() £ї£®2£©
£ї£®2£©![]() £ї£®3£©
£ї£®3£©![]() £Ѓ
£Ѓ
°Њљвќц°њ
£®1£© „ѕ»«у≥цµгB°ҐCµƒ„ш±к£ђ»їЇујы”√іэґ®ѕµ эЈ®«у≥ц≈„ќпѕяµƒљвќц љ£ї
£®2£©ЄщЊЁS°чABC=S°чAMC+S°чAMB£ђ”…»эљ«–ќ√жїэєЂ љњ…«уy”лm÷ЃЉдµƒЇѓ эєЎѕµ љ£ї
£®3£©»зЌЉ2£ђ”…≈„ќпѕяґ‘≥∆–‘њ…µ√D£®2£ђ-3£©£ђєэµгB„чBK°ЌCDљї÷±ѕяCD”ЏµгK£ђOG°ЌOSљїKB”ЏG£ђњ…µ√Ћƒ±я–ќOCKBќ™’эЈљ–ќ£ђєэµгO„чOH°ЌPCљїPC—”≥§ѕя”ЏµгH£ђOR°ЌBQљїBQ”ЏµгIљїBK”ЏµгR£ђњ…µ√Ћƒ±я–ќOHQIќ™ЊЎ–ќ£ђњ…÷§°чOBG°’°чOCS£ђ°чOSR°’°чOGR£ђµ√µљtan°ѕQCT=tan°ѕTBK£ђ…иST=TD=m£ђњ…µ√SK=2m+1£ђCS=2-2m£ђTK=m+1=BR£ђSR=3-m£ђRK=2-m£ђ‘ЏRt°чSKR÷–£ђЄщЊЁєіє…ґ®јн«уµ√m£ђњ…µ√tan°ѕPCD=![]() £ђєэµгP„чPE°д°Ќx÷б”ЏE°дљїCD”ЏµгF°д£ђµ√µљP£®t£ђ-
£ђєэµгP„чPE°д°Ќx÷б”ЏE°дљїCD”ЏµгF°д£ђµ√µљP£®t£ђ-![]() t-3£©£ђњ…µ√-
t-3£©£ђњ…µ√-![]() t-3=t2-2t-3£ђ«уµ√t£ђ‘ўЄщЊЁMN=d«уљвЉіњ…£Ѓ
t-3=t2-2t-3£ђ«уµ√t£ђ‘ўЄщЊЁMN=d«уљвЉіњ…£Ѓ
љв£Ї£®1£©°я÷±ѕяy=x-3Њ≠єэB°ҐCЅљµг£ђ
°аB£®3£ђ0£©£ђC£®0£ђ-3£©£ђ
°яy=x2+bx+cЊ≠єэB°ҐCЅљµг£ђ
°а![]() £ђ
£ђ
љвµ√![]() £ђ
£ђ
є ≈„ќпѕяµƒљвќц љќ™y=x2-2x-3£ї
£®2£©»зЌЉ1£ђy=x2-2x-3£ђ
y=0 ±£ђx2-2x-3=0£ђ
љвµ√x1=-1£ђx2=3£ђ
°аA£®-1£ђ0£©£ђ
°аOA=1£ђOB=OC=3£ђ
°а°ѕABC=45°г£ђAC=![]() £ђAB=4£ђ
£ђAB=4£ђ
°яPE°Ќx÷б£ђ
°а°ѕEMB=°ѕEBM=45°г£ђ
°яµгPµƒЇб„ш±кќ™t£ђ
°аEM=EB=3-t£ђ
Ѕђљ”AM£ђ
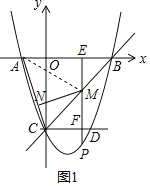
°яS°чABC=S°чAMC+S°чAMB
![]()
![]() £ђ
£ђ
°а![]() £ї
£ї
£®3£©»зЌЉ2£ђ
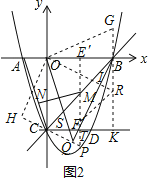
°яy=x2-2x-3=£®x-1£©2-4£ђ
°аґ‘≥∆÷бќ™x=1£ђ
°а”…≈„ќпѕяґ‘≥∆–‘њ…µ√D£®2£ђ-3£©£ђ
°аCD=2£ђ
єэµгB„чBK°ЌCDљї÷±ѕяCD”ЏµгK£ђ
°аЋƒ±я–ќOCKBќ™’эЈљ–ќ£ђ
°а°ѕOBK=90°г£ђCK=OB=BK=3£ђ
°аDK=1£ђ
°яBQ°ЌCP£ђ
°а°ѕCQB=90°г£ђ
°я°ѕCQB+°ѕCOB=180°г£ђ
°аO°ҐC°ҐQ°ҐBЋƒµгє≤‘≤£ђ
°а°ѕOQB=°ѕOCB=45°г
єэµгO„чOH°ЌPCљїPC—”≥§ѕя”ЏµгH£ђOR°ЌBQљїBQ”ЏµгIљїBK”ЏµгR£ђOG°ЌOSљїKB”ЏG£ђ
°а°ѕOHC=°ѕOIQ=°ѕOIB=90°г£ђ
°аЋƒ±я–ќOHQIќ™ЊЎ–ќ£ђ
°я°ѕOQI=45°г£ђ
°а°ѕOQI=°ѕIOQ=45°г£ђ
°я°ѕOCQ+°ѕOBQ=180°г£ђ
°а°ѕOBG=°ѕOCS£ђ
°яOB=OC£ђ°ѕBOG=°ѕCOS£ђ
°а°чOBG°’°чOCS£ђ
°аQG=OS£ђ°ѕGOB=°ѕSOC£ђ
°а°ѕSOG=90°г£ђ
°а°ѕROG=°ѕQOI=45°г£ђ
°яOR=OR£ђ
°а°чOSR°’°чOGR£ђ
°аSR=GR£ђ
°аSR=CS+BR£ђ
°я°ѕBOR+°ѕOBI=90°г£ђ°ѕIBO+°ѕTBK=90°г£ђ
°а°ѕBOR=°ѕTBK£ђ
°аtan°ѕBOR=tan°ѕTBK£ђ
°а![]() £ђ
£ђ
°аBR=TK£ђ
°я°ѕCTQ=°ѕBTK£ђ
°а°ѕQCT=°ѕTBK£ђ
°аtan°ѕQCT=tan°ѕTBK£ђ
…иST=TD=m£ђ
°аSK=2m+1£ђCS=2-2m£ђTK=m+1=BR£ђSR=3-m£ђRK=2-m£ђ
‘ЏRt°чSKR÷–£ђ
°яSK2+RK2=SR2£ђ
°а£®2m+1£©2+£®2-m£©2=£®3-m£©2£ђ
љвµ√m1=-2£®…б»•£©£ђm2=![]() £ї
£ї
°аST=TD=![]() £ђTK=
£ђTK=![]() £ђ
£ђ
°аtan°ѕTBK=![]() £ђ
£ђ
°аtan°ѕPCD=![]() £ђ
£ђ
єэµгP„чPE°д°Ќx÷б”ЏE°дљїCD”ЏµгF°д£ђ
°яCF°д=OE°д=t£ђ
°аPF°д=![]() t£ђ
t£ђ
°аPE°д=![]() t+3£ђ
t+3£ђ
°аP£®t£ђ-![]() t-3£©£ђ
t-3£©£ђ
°а-![]() t-3=t2-2t-3£ђ
t-3=t2-2t-3£ђ
љвµ√t1=0£®…б»•£©£ђt2=![]() £Ѓ
£Ѓ
°аMN=d=![]() £Ѓ
£Ѓ