��Ŀ����
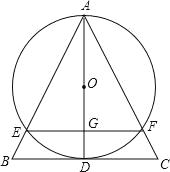
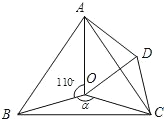
����Ŀ����һ�����dz߰�ͼ1�ڷţ�����ֱ�����dzߵ�ֱ�DZ�DFǡ�ô�ֱƽ��AB����AC�ཻ�ڵ�G��![]() ��
��
��1����GC�ij���
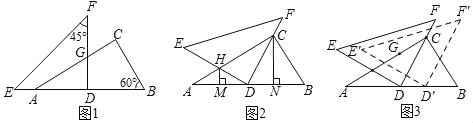
��2����ͼ2������DEF�Ƶ�D˳ʱ����ת��ʹֱ�DZ�DF������C����һֱ�DZ�DE��AC�ཻ�ڵ�H���ֱ��H��C��AB�Ĵ��ߣ�����ֱ�ΪM��N��ͨ���۲죬����MD��ND��������ϵ������֤��IJ��룮
��3���ڣ�2���������£�����DEF��DB����ƽ�Ƶõ���D��E��F�䣬��D��E��ǡ�þ�����1���еĵ�Gʱ����ֱ��д��DD��ij��ȣ�
���𰸡���1��2����2��DM=DN����3��![]()
��������
��1����ֱ�����������AC��AG���ɽ�����⣻
��2����ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬�õ�CD=BD=AD�����ɡ�B=60�㣬�õ���BDCΪ�ȱ������Σ��Ӷ�����֤����HDA=30�㣬��һ���õ� AH=HD���ɵ��������ε����ʵõ�MD=AM��ND=NB�����ɵõ����ۣ�
��3����ͼ3�У���GK��DE��AB��K�����AK��ֵ���ɽ�����⣮
��1����ͼ1��
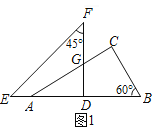
��Rt��ABC�У���BC=2![]() ����B=60�㣬��AC=BCtan60��=6��AB=2BC=4
����B=60�㣬��AC=BCtan60��=6��AB=2BC=4![]() ��
��
��DF���߶�AB�Ĵ�ֱƽ���ߣ���AD=BD=2![]() ��
��
��Rt��ADG��AG![]() 4����CG=AC=AG=6��4=2��
4����CG=AC=AG=6��4=2��
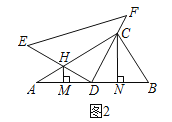
��2����ͼ2�У����ۣ�DM=DN��
���ɣ��ߡ�ABCΪֱ�������Σ�DΪб��AB���е㣬��CD=BD=AD��
�֡�B=60�㣬���BDCΪ�ȱ������Σ����CDB=60�㣮
�֡�EDF=90�㣬���HDA=30�㣮
�ߡ�A=90�㩁��B=30�㣬��AH=HD����HM��AD����MD=AM��
�ڵȱ������� BCD�У�CN��BD����ND=NB��
��AD=BD����MD=ND��
��3����ͼ3�У���GK��DE��AB��K��
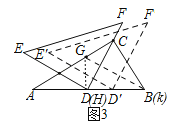
�ڡ�AGK�У�AG=GK=4����A=��GKD=30�㣬��GH��AB��H��
��AH=AGcos30��=2![]() ���ɵ�AK=2AH=4
���ɵ�AK=2AH=4![]() ����ʱK��B�غϣ���DD��=DB=2
����ʱK��B�غϣ���DD��=DB=2![]() ��
��