题目内容
如图，函数y=-
x+2的图象交y轴于M，交x轴于N，线段MN上的两点A，B在x轴上射影分别为A1，B1，若OA1+OB1＞4，OA1＜OB1，则△OA1A的面积S1与△OB1B的面积S2的大小关系是
- A.S1＞S2
- B.S1=S2
- C.S1＜S2
- D.不能确定
A
分析：设OA1长为x，OA2长为y，可分别求出对应的纵坐标，从而可求出两个三角形的面积，用作差法判断面积的大小．
解答：设OA1长为x，OA2长为y，
AA1=-x+2，BB1=-y+2．
-
=（x-y）[-
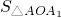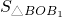（x+y）+1]＞0．
∴S1＞S2．
故选A．
点评：本题考查一次函数的综合题，关键是表示出两个三角形的面积，用作差法求解．
分析：设OA1长为x，OA2长为y，可分别求出对应的纵坐标，从而可求出两个三角形的面积，用作差法判断面积的大小．
解答：设OA1长为x，OA2长为y，
AA1=-
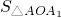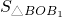x+2，BB1=-y+2．-=（x-y）[-（x+y）+1]＞0．∴S1＞S2．
故选A．
点评：本题考查一次函数的综合题，关键是表示出两个三角形的面积，用作差法求解．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
如图：函数y=-kx（k≠0）与y=-
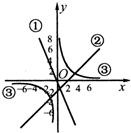如图，函数图象①、②、③的表达式应为（ ）A、y=-
| ||||
B、y=
| ||||
C、y=-
| ||||
D、y=-
|
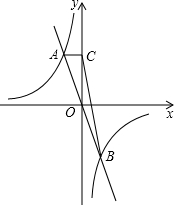如图，函数y=-kx与
如图，函数y1=k1x+b的图象与函数y2=