题目内容
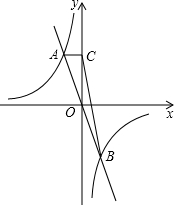 如图,函数y=-kx与y=-
如图,函数y=-kx与y=-| 4 | x |
分析:由于函数y=-kx与y=-
交于A、B两点,所以点A与点B关于原点O对称,则S△BCO=S△ACO,再根据反比例函数系数k的几何意义,可知S△ACO=2,从而得出S△BCO的值.
| 4 |
| x |
解答:解:∵函数y=-kx与y=-
交于A、B两点,
∴点A与点B关于原点O对称,
∴S△BCO=S△ACO.
又∵AC垂直y轴于点C,
∴S△ACO=
|k|=2,
∴S△BCO=2.
| 4 |
| x |
∴点A与点B关于原点O对称,
∴S△BCO=S△ACO.
又∵AC垂直y轴于点C,
∴S△ACO=
| 1 |
| 2 |
∴S△BCO=2.
点评:本题主要考查了反比例函数的图象性质以及比例系数k的几何意义.由于反比例函数是中心对称图形,对称中心是原点O,所以当正比例函数图象与反比例函数的图象相交时,两个交点一定关于原点O对称;过双曲线y=
上的任意一点向坐标轴作垂线,这一点与原点、垂足围成的三角形的面积等于
|k|.
| k |
| x |
| 1 |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
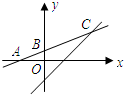 如图,函数y=kx+b的图象与x轴,y轴分别交于A(-2,0),B(0,1)两点,那么此函数的图象与函数y=x-1的图象交点C的坐标是
如图,函数y=kx+b的图象与x轴,y轴分别交于A(-2,0),B(0,1)两点,那么此函数的图象与函数y=x-1的图象交点C的坐标是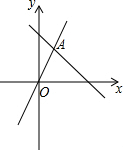 (2013•鄞州区模拟)如图,函数y=kx和y=-
(2013•鄞州区模拟)如图,函数y=kx和y=- 如图,函数y=
如图,函数y=