题目内容
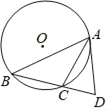
【题目】如图,⊙O是△ABC的外接圆,过点A作⊙O的切线交BC的延长线于点D.
(1)求证:∠CAD=∠B.
(2)若AC是∠BAD的平分线,sinB=![]() ,BC=2.求⊙O的半径.
,BC=2.求⊙O的半径.
【答案】(1)见解析;(2)⊙O的半径为![]() .
.
【解析】
(1)连结AO,并延长AO交⊙O与点E,连结EC,依据圆周角定理可得到∠B=∠E,然后根据直径所对的圆周角为90°,得出∠E+∠EAC=90°,再根据切线的性质可得∠EAC+∠CAD=90°,进行证明即可;
(2)根据AC是∠BAD的平分线,结合(1)中结论证出BC=AC,然后由∠B=∠E可得到sinE=![]() ,从而可求得AE的长,然后可求得⊙O的半径.
,从而可求得AE的长,然后可求得⊙O的半径.
解:(1)连结AO,并延长AO交⊙O与点E,连结EC.

∵AD为⊙O的切线,
∴OA⊥AD,
∴∠EAD=90°,
∴∠EAC+∠CAD=90°.
∵AE为⊙O的直径,
∴∠E+∠EAC=90°,
∴∠E=∠CAD.
又∵∠E=∠B,
∴∠CAD=∠B.
(2)∵AC是∠BAD的平分线,
∴∠BAC=∠CAD.
又∵∠CAD=∠B,
∴∠BAC=∠CAB.
∴AC=BC=2.
又∵∠E=∠B,
∴∠CAD=∠B.
∴sinE=sinB=![]() ,
,
在Rt![]() AEC中,sinE=
AEC中,sinE=![]() ,
,
即![]() =
=![]() ,解得AE=
,解得AE=![]() ,
,
∴⊙O的半径为![]() .
.

练习册系列答案
相关题目