Question

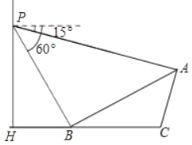
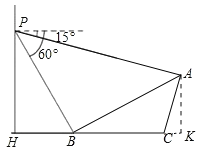
【题目】如图，小华在体育馆的看台P处进行观测，测得另一看台观众A处的俯角为15°，观众B处的俯角为60°，已知观众A、B所在看台的坡度i(即tan∠ABC)为1：，点P、H、B、C、A在同一个平面上，点H、B、C在同一条直线上，且PH⊥HC，PH＝15米．

(1)AB所在看台坡角∠ABC＝____度；

(2)求A、B两点间的距离．(结果精确到0.1米，参考数据：≈1.73)

Answer 1

【答案】(1)30；(2)AB≈17.3m.

【解析】

（1）作交的延长线于，根据坡度的定义求出的值即可求得答案.

（2）证明，求出即可求得答案.

解：（1）作交的延长线于，如下图所示，

由题意： ，

∴ ，

故答案为．

(2)由题意，，

∵ ，

∴ ，

∵ ，

∴ ，

∴ ，

∴ ，

在中，∵ ，

∴ ，

∴ ．