��Ŀ����
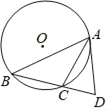
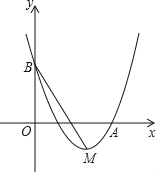
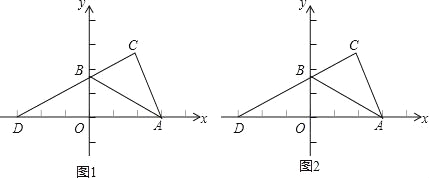
����Ŀ����ͼ��Rt��AOB��ƽ��ֱ������ϵ�У���֪��B��0��![]() ������A��x����������ϣ�OA=3����BAD=30�㣬����AOB��AB���ۣ���O����C��λ�ã�����CB���ӳ���x���ڵ�D��
������A��x����������ϣ�OA=3����BAD=30�㣬����AOB��AB���ۣ���O����C��λ�ã�����CB���ӳ���x���ڵ�D��
��1�����D�����ꣻ
��2������P�ӵ�D��������ÿ��2����λ���ٶ���x����������˶�������PABΪֱ��������ʱ����t��ֵ��
��3���ڣ�2���������£�����PABΪ�ԡ�PBAΪֱ�ǵ�ֱ��������ʱ����y�����Ƿ����һ��Qʹ��PBQΪ���������Σ�������ڣ���ֱ��д��Q������ꣻ��������ڣ���˵�����ɣ�
���𰸡���1��D����3��0������2��![]() ����3��Q������ΪQ1��0��
����3��Q������ΪQ1��0��![]() +2����Q2��0��
+2����Q2��0��![]() ����Q3��0��
����Q3��0��![]() ��2����Q4��0����
��2����Q4��0����![]() ����
����
��������
��1��������֪�ó�OA��OB��ֵ�Լ���DAC�Ķ��������������ADC���������D�����ꣻ
��2������ֱ�������ε��ж������������������ã�
��3�����PB�ij����������������ۼ��ɽ�����⣮
�⣺��1����B��0��![]() ����
����
��OB=![]() ��
��
��OA=![]() OB��
OB��
��OA=3��
��AC=3��
�ߡ�BAD=30����
���OAC=60����
�ߡ�ACD=90����
���ODB=30����
��![]() =
=![]() ��
��
��OD=3��
��D����3��0����
��2����OA=3��OD=3����A��3��0����AD=6��
��AB=2![]() ������PBA=90��ʱ��
������PBA=90��ʱ��
��PD=2t��
��OP=3��2t��
�ߡ�OBA�ס�OPB��
��OB2=OPOA��
��3��2t=![]() =1�����t=1������APB=90��ʱ����P��O�غϣ�
=1�����t=1������APB=90��ʱ����P��O�غϣ�
��t=![]() ��
��
��3�����ڣ�

����BPΪ���ĵ��������Σ�
��OP=1����BP=![]() =2��
=2��
��Q1��0��![]() +2����Q3��0��
+2����Q3��0��![]() ��2����
��2����
����PQ2=Q2Bʱ����PQ2=Q2B=a��
��Rt��OPQ2��12+��![]() ��x��2=x2�����x=
��x��2=x2�����x=![]() ��
��
��Q2��0��![]() ����
����
����PB=PQ4ʱ��Q4��0����![]() ��
��
�������������������ĵ�Q������ΪQ1��0��![]() +2����Q2��0��
+2����Q2��0��![]() ����Q3��0��
����Q3��0��![]() ��2����Q4��0����
��2����Q4��0����![]() ����
����

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�����Ŀ������ʦ��![]() ����������ɸ��������һ�������Ŀڴ������ȣ�������ѧ����������ʵ�飬ÿ������һ�����зŻأ����±��ǻ�����е�һ��ͳ�����ݣ�
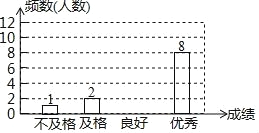
����������ɸ��������һ�������Ŀڴ������ȣ�������ѧ����������ʵ�飬ÿ������һ�����зŻأ����±��ǻ�����е�һ��ͳ�����ݣ�
����Ĵ��� |
|
|
|
|
|
|
��������Ĵ��� |
|
|
|
|
|
|
���������Ƶ�� |
|
|
|
|
|
![]() ��ȫ�ϱ��е��й����ݣ������ϱ����ݹ��ƴӴ�������һ�����Ǻ���ĸ�����________����ȷ��0.01����
��ȫ�ϱ��е��й����ݣ������ϱ����ݹ��ƴӴ�������һ�����Ǻ���ĸ�����________����ȷ��0.01����
![]() ������а���ĸ�����
������а���ĸ�����
![]() ��
��![]() �������£���Сǿͬѧ�зŻص��������������û���״ͼ���б��ķ������������ζ���������ĸ��ʣ�
�������£���Сǿͬѧ�зŻص��������������û���״ͼ���б��ķ������������ζ���������ĸ��ʣ�