题目内容
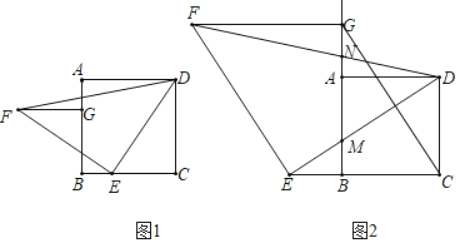
【题目】如图1,在正方形ABCD中,E是边BC上的点,将线段DE绕点E逆时针旋转90°得到EF,过点C作CG∥EF交BA(或其延长线)于点G,连接DF,FG.
(1)FG与CE的数量关系是 ,位置关系是 .
(2)如图2,若点E是CB延长线上的点,其它条件不变.
①(1)中的结论是否仍然成立?请作出判断,并给予证明;
②DE,DF分别交BG于点M,N,若BC=2BE,求![]() .
.
【答案】(1)FG=EC,FG∥EC.(2)①结论不变,见解析,②![]() =
=![]() .
.
【解析】
(1)结论:FG=EC,FG∥EC.证明四边形ECGF是平行四边形即可.
(2)①结论不变.证明四边形ECGF是平行四边形即可.
②如图2-1中,延长AG到H,使得AH=AD,连接DH,BD,在BC上截取一点K,使得BK=HN,连接MK,DK.首先证明MB=BK,设BC=a,MN=b,求出BM,BK,在Rt△BMK中,利用勾股定理即可解决问题.
解:(1)结论:FG=EC,FG∥EC.
理由:如图1中,
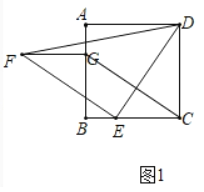
∵四边形ABCD是正方形,
∴BC=CD,∠CBG=∠DCE=90°,
∵∠DEF=90°,
∴∠FEB+∠DEC=90°,∠DEC+∠EDC=90°,
∴∠FEB=∠EDC,
∵CG∥EF,
∴∠GCB=∠FEB=∠EDC,
∴△GCB≌△EDC(ASA),
∴CG=DE,
∵EF=DE,
∴CG=EF,∵CG∥EF,
∴四边形ECGF是平行四边形,
∴FG=EC,FG∥EC.
(2)①结论不变.
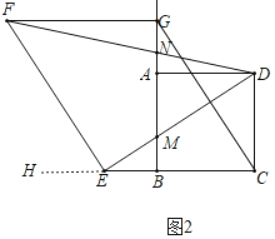
理由:延长CE到H.
∵四边形ABCD是正方形,
∴BC=CD,∠CBG=∠DCE=90°,
∵∠DEF=90°,
∴∠FEH+∠DEC=90°,∠DEC+∠EDC=90°,
∴∠FEH=∠EDC,
∵CG∥EF,
∴∠GCB=∠FEH=∠EDC,
∴△GCB≌△EDC(ASA),
∴CG=DE,
∵EF=DE,
∴CG=EF,∵CG∥EF,
∴四边形ECGF是平行四边形,
∴FG=EC,FG∥EC.
②如图2﹣1中,延长AG到H,使得AH=AD,连接DH,BD,在BC上截取一点K,使得BK=HN,连接MK,DK.
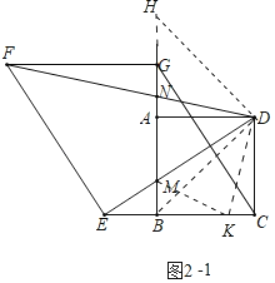
∵AH=AD=AB,DA⊥BH,
∴DH=DB,∠HDB=90°,
∵BK=HN,∠H=∠DBK=45°,
∴△NHD≌△KBD(SAS),
∴DN=DK,∠HDN=∠BDK,
∴∠HDB=∠NDK=90°,
∵∠MDN=45°,
∴∠NDM=∠KDM=45°,
∵DM=DM,
∴△NDM≌△KDM,
∴MN=MK,设BC=a,MN=b,
∵BC=2BE,
∴EB=![]() a,
a,
∵
∴![]() ,
,
∴BM=![]() a,
a,
∵BK=NH=2a﹣![]() a﹣b=
a﹣b=![]() a﹣b,
a﹣b,
在Rt△BMK中,∵MK2=BM2+BK2,
∴b2=(![]() a)2+(
a)2+(![]() a﹣b)2,
a﹣b)2,
整理得:![]() =
=![]() ,
,
∴![]() .
.
故答案为:(1)FG=EC,FG∥EC.(2)①结论不变,见解析,②![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:千帕)随气体体积V(单位:立方米)的变化而变化,P随V的变化情况如下表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出符合表格数据的P关于V的函数表达式 ;
(2)当气球的体积为20立方米时,气球内气体的气压P为多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数表达式,基于安全考虑,气球的体积至少为多少立方米?