题目内容
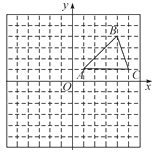
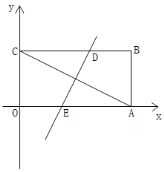
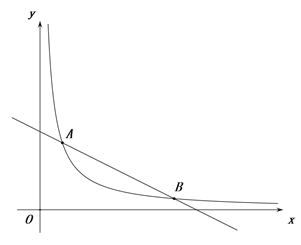
【题目】如图,一次函数y=-![]() x+b与反比例函数y=
x+b与反比例函数y=![]() (x>0)的图象交于点A(2,6)和B(m,1)
(x>0)的图象交于点A(2,6)和B(m,1)
(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
【答案】(1)y=﹣![]() x+7,y=
x+7,y=![]() (2)(0,6)或(0,8)
(2)(0,6)或(0,8)
【解析】分析:(1)把点A的坐标分别代入一次函数y与反比例函数,可得b,k的值,从而得到结论.
(2)把B(m,1)代入反比例函数,得到m的值,从而得到B的坐标.设直线AB与y轴的交点为P,点E的坐标为(0,a),连接AE,BE,则点P的坐标为(0,7),得到PE=|a﹣7|.由S△AEB=S△BEP﹣S△AEP=5, 可求得a的值,从而得到点E的坐标.
详解:(1)∵一次函数y=-![]() x+b与反比例函数y=
x+b与反比例函数y=![]() (x>0)的图象交于点A(2,6),∴6=
(x>0)的图象交于点A(2,6),∴6=![]() ,k=2×6=12,解得:b=7,k=12.∴一次函数的解析式为
,k=2×6=12,解得:b=7,k=12.∴一次函数的解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() .
.
(2)∵B(m,1)在反比例函数![]() 上,∴1=
上,∴1=![]() ,解得:m=12,∴B(12,1).
,解得:m=12,∴B(12,1).
如图,直线AB与y轴的交点为P,设点E的坐标为(0,a),连接AE,BE,
则点P的坐标为(0,7).
∴PE=|a﹣7|.
∵S△AEB=S△BEP﹣S△AEP=5,
∴![]() ×|a﹣7|×(12﹣2)=5.
×|a﹣7|×(12﹣2)=5.
∴|a﹣7|=1.
∴a1=6,a2=8.
∴点E的坐标为(0,6)或(0,8).


练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目