Question

【题目】如图，在四边形ABCD中，∠DBC=90°，∠ABD=30°，∠ADB=75°，AC与BD交于点E，若CE=2AE=4，则DC的长为________．

Answer 1

【答案】

【解析】

过A点作A⊥BD于F，根据平行线的判定可得AF∥BC，根据含30度直角三角形的性质可得BC=AB，根据三角形内角和可得∠ADB=∠BAD，根据等腰三角形的性质可得BD=AB，从而得到BC=BD，在Rt△CBE中，根据含30度直角三角形的性质可得BC，在Rt△CBD中，根据等腰直角三角形的性质可得CD．

过A点作A⊥BD于F，

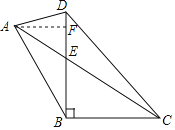
∵∠DBC=90°，

∴AF∥BC，

∵CE=2AE，

∴AF=BC，

∵∠ABD=30°，

∴AF=AB，

∴BC=AB，

∵∠ABD=30°，∠ADB=75°，

∴∠BAD=75°，∠ACB=30°，

∴∠ADB=∠BAD，

∴BD=AB，

∴BC=BD，

∵CE=4，

在Rt△CBE中，BC=CE=6，

在Rt△CBD中，CD=BC=6．

故答案为：6．