Question

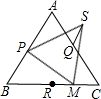
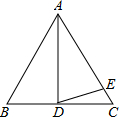
如图，等边三角形ABC中，AB=4，点P是AB上的一个动点（点P可以与点A重合，但不与点B重合），过点P作PE⊥BC，垂足为，过点E作EF⊥AC，垂足为F，过点F作FQ⊥AB，垂足为Q，设BP=x，AQ=y．
（1）写出y与x之间的函数关系式及自变量x的取值范围；
（2）当BP的长等于多少时，点P与点Q重合；
（3）用x的代数式表示PQ的长（不必写出解题过程）．

Answer 1

（1）PE⊥BC，EF⊥AC，FQ⊥AB，
∠A=∠B=∠C=60°，设BP=x，
∴BE=

x

2

，EC=4-

x

2

，CF=2-

x

4

，
AF=4-2+

x

4

=2+

x

4

，
∵△BEP∽△AQF，
∴

AF

BP

=

AQ

BE

，
∴AQ=1+

x

8

，
∴y=1+

x

8

（0＜x≤4）；

（2）当x+y=4，x+1+

x

8

=4，
∴

9

8

x=3，
∴x=

8

3

，
故BP为

8

3

时，P与Q重合；

（3）PQ=3-

9

8

x(0＜x≤

8

3

)，
PQ=

9

8

x-3(

8

3

＜x≤4)．