题目内容

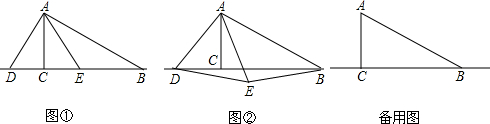
如图，AD是等边△ABC的中线，E是AC上一点，且AD=AE，则∠EDC=______°．
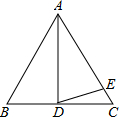
∵AD是等边△ABC的中线，
∴AD⊥BC，∠BAD=∠CAD=
1
2
∠BAC=
1
2
×60°=30°，
∴∠ADC=90°，
∵AD=AE，
∴∠ADE=∠AED=
180°-∠CAD
2
=75°，
∴∠EDC=∠ADC-∠ADE=90°-75°=15°．
故答案为：15．
练习册系列答案
相关题目
等边三角形的面积为8
3
，它的高为（　　）
A．2
2
B．4
3
C．2
6
D．2
5
如图，等边三角形ABC中，AB=4，点P是AB上的一个动点（点P可以与点A重合，但不与点B重合），过点P作PE⊥BC，垂足为，过点E作EF⊥AC，垂足为F，过点F作FQ⊥AB，垂足为Q，设BP=x，AQ=y．
（1）写出y与x之间的函数关系式及自变量x的取值范围；
（2）当BP的长等于多少时，点P与点Q重合；
（3）用x的代数式表示PQ的长（不必写出解题过程）．
如图，直角坐标系中，点A的坐标为（a，0），以线段OA为边在第四象限内作等边△AOB，点C为x正半轴上一动点（OC＞a＞0），连接BC，以线段BC为边在第四象限内作等边△CBD，直线DA交y轴于点E．
（1）求证：OC=AD．
（2）随着点C位置的变化，点E的位置是否会发生变化？若没有变化，求出点E的坐标；若有变化，请说明理由．
（3）当C点运动到使OA：AC=1：3时，求出此时D点的坐标．
如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°．点D是直线BC上的一个动点，连接AD，并以AD为边在AD的右侧作等边△ADE．
（1）如图①，当点E恰好在线段BC上时，请判断线段DE和BE的数量关系，并结合图①证明你的结论；
（2）当点E不在直线BC上时，连接BE，其它条件不变，（1）中结论是否成立？若成立，请结合图②给予证明；若不成立，请直接写出新的结论；
（3）若AC=3，点D在直线BC上移动的过程中，是否存在以A、C、D、E为顶点的四边形是梯形？如果存在，直接写出线段CD的长度；如果不存在，请说明理由．
如图，已知：∠MON=30°，点A1、A2、A3在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=1，则△A6B6A7的边长为______．
如图，在边长为20cm的等边三角形ABC纸片中，以顶点C为圆心，以此三角形的高为半径画弧分别交AC、BC于点D、E，则扇形CDE所围的圆锥（不计接缝）的底圆半径为（　　）
A．
5
3
3
cm		B．
10
3
3
cm		C．5
3
cm		D．10
3
cm
如图：△ABC是等边三角形?
（1）若AD=BE=CF，求证△DEF是等边三角形．?
（2）请问（1）的逆命题成立吗？若成立，请证明，若不成立，请用反例说明?
如图，在直角坐标系中，△AOB是等边三角形，若B点的坐标是（2，0），则A点的坐标是（　　）
A．（2，1）B．（1，2）C．（
3
，1）		D．（1，
3
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网