题目内容
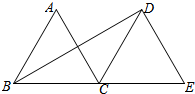
如图，△ABC和△DCE都是边长为6的等边三角形，点B，C，E在同一条直线上，连接BD，则BD的长为（ ）
A．2
| B．4 | C．4
| D．6
|
∵△ABC与△DCE都是边长为6的等边三角形，
∴∠ACB=∠DCE=60°，BC=CD=6，
∴∠ACD=180°-（∠ACB+∠DCE）=60°，
∴∠ACB=∠ACD，即CF为∠BCD的平分线，
∴CF⊥BD，BF=DF，
在Rt△BFC中，∠BCF=60°，BC=6，
∴BF=BCsin60°=3
，
则BD=2BF=6
．
故选D
∴∠ACB=∠DCE=60°，BC=CD=6，
∴∠ACD=180°-（∠ACB+∠DCE）=60°，
∴∠ACB=∠ACD，即CF为∠BCD的平分线，
∴CF⊥BD，BF=DF，
在Rt△BFC中，∠BCF=60°，BC=6，
∴BF=BCsin60°=3
| 3 |
则BD=2BF=6
| 3 |
故选D
练习册系列答案
名校课堂系列答案
相关题目
