题目内容
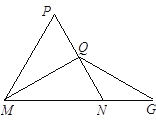
【题目】如下图，△MNP中，∠P=60°，MN=NP，MQ⊥PN，垂足为Q，延长MN至G，取NG=NQ，若△MNP的周长为12，MQ=a，则△MGQ周长是（ ）
A. 8+2a B. 8+a C. 6+a D. 6+2a
【答案】D
【解析】
试题由∠P=60°，MN=NP，可得△MNP是等边三角形，再根据等边三角形的“三线合一”的性质以及等腰三角形的判定，即可求得结果。
∵∠P=60°，MN=NP
∴△MNP是等边三角形．
又∵MQ⊥PN，垂足为Q，
∴PM=PN=MN=4，NQ=NG=2，MQ=a，∠QMN=30°，∠PNM=60°，
∵NG=NQ，
∴∠G=∠QMN，
∴QG=MQ=a，
∵△MNP的周长为12，
∴MN=4，NG=2，
∴△MGQ周长是6+2a．
故选D．
练习册系列答案
相关题目
