题目内容
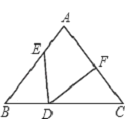
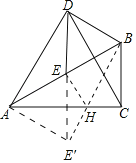
【题目】如图,在Rt△ABC中,(M2,N2),∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
(1)求证:△ADE≌△CDB;
(2)若BC=![]() ,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.

【答案】(1)证明见解析;(2)BH+EH的最小值为3.
【解析】
(1)只要证明△DEB是等边三角形,再根据SAS即可证明;
(2)如图,作点E关于直线AC点E',连接BE'交AC于点H.则点H即为符合条件的点.
(1)在Rt△ABC中,∠BAC=30°,E为AB边的中点,
∴BC=EA,∠ABC=60°,
∵△DEB为等边三角形,
∴DB=DE,∠DEB=∠DBE=60°,
∴∠DEA=120°,∠DBC=120°,
∴∠DEA=∠DBC,
∴△ADE≌△CDB;
(2)如图,作点E关于直线AC点E',连接BE'交AC于点H,则点H即为符合条件的点,
由作图可知:EH=HE',AE'=AE,∠E'AC=∠BAC=30°,
∴∠EAE'=60°,
∴△EAE'为等边三角形,
∴E E'=EA=![]() AB,
AB,
∴∠AE'B=90°,
在Rt△ABC中,∠BAC=30°,BC=![]() ,
,
∴AB=2![]() ,A E'=AE=
,A E'=AE=![]() ,
,
∴B E'=![]() =3,
=3,
∴BH+EH的最小值为3.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目