题目内容
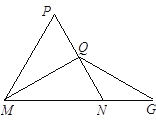
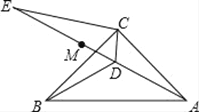
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN. 
(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME,
∵点E是AD中点,
∴DE=AE,
在△NDE和△MAE中,
 ,
,
∴△NDE≌△MAE(AAS),
∴ND=MA,
∴四边形AMDN是平行四边形
(2)AM=1.
理由如下:∵四边形ABCD是菱形,
∴AD=AB=2,
∵平行四边形AMDN是矩形,
∴DM⊥AB,
即∠DMA=90°,
∵∠DAB=60°,
∴∠ADM=30°,
∴AM= ![]() AD=1
AD=1
【解析】(1)根据菱形的性质可得ND∥AM,再根据两直线平行,内错角相等可得∠NDE=∠MAE,∠DNE=∠AME,根据中点的定义求出DE=AE,然后利用“角角边”证明△NDE和△MAE全等,根据全等三角形对应边相等得到ND=MA,然后利用一组对边平行且相等的四边形是平行四边形证明;(2)根据矩形的性质得到DM⊥AB,再求出∠ADM=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目