ћвƒњƒЏ»Ё
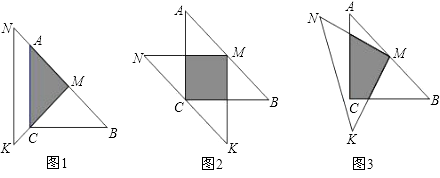
°Њћвƒњ°њ»зЌЉ£ђµ»—ьRt°чABC÷–£ђ°ѕACB=90°г£ђAC=BC=1£ђ«“AC±я‘Џ÷±ѕяa…ѕ£ђљЂ°чABC»∆µгAЋ≥ ±’л–э„™µљќї÷√Ґўњ…µ√µљµгP1 £ђ іЋ ±AP1= ![]() £їљЂќї÷√Ґўµƒ»эљ«–ќ»∆µгP1Ћ≥ ±’л–э„™µљќї÷√ҐЏњ…µ√µљµгP2 £ђ іЋ ±AP2=
£їљЂќї÷√Ґўµƒ»эљ«–ќ»∆µгP1Ћ≥ ±’л–э„™µљќї÷√ҐЏњ…µ√µљµгP2 £ђ іЋ ±AP2= ![]() +1£їљЂќї÷√ҐЏµƒ»эљ«–ќ»∆µгP2Ћ≥ ±’л–э„™µљќї÷√Ґџњ…µ√µљµгP3 ±£ђAP3=
+1£їљЂќї÷√ҐЏµƒ»эљ«–ќ»∆µгP2Ћ≥ ±’л–э„™µљќї÷√Ґџњ…µ√µљµгP3 ±£ђAP3= ![]() +2°≠∞ііЋєж¬…Љћ–ш–э„™£ђ÷±÷Ѕµ√µљµгP2026ќ™÷є£ђ‘тAP2016= £Ѓ
+2°≠∞ііЋєж¬…Љћ–ш–э„™£ђ÷±÷Ѕµ√µљµгP2026ќ™÷є£ђ‘тAP2016= £Ѓ 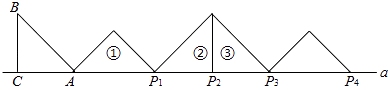
°Њір∞Є°њ1344+672 ![]()
°Њљвќц°њљв£ЇAP1= ![]() £ђAP2=1+
£ђAP2=1+ ![]() £ђAP3=2+
£ђAP3=2+ ![]() £ї
£ї
AP4=2+2 ![]() £їAP5=3+2
£їAP5=3+2 ![]() £їAP6=4+2
£їAP6=4+2 ![]() £ї
£ї
AP7=4+3 ![]() £їAP8=5+3
£їAP8=5+3 ![]() £їAP9=6+3
£їAP9=6+3 ![]() £ї
£ї
°я2016=3°Ѕ672£ђ
°аAP2013=£®2013©Б671£©+671 ![]() =1342+671
=1342+671 ![]() £ђ
£ђ
°аAP2014=1342+671 ![]() +
+ ![]() =1342+672
=1342+672 ![]() £ђ
£ђ
°аAP2015=1342+672 ![]() +1=1343+672
+1=1343+672 ![]() £ђ
£ђ
°аAP2016=1343+672 ![]() +1=1344+672
+1=1344+672 ![]() £ђ
£ђ
є ір∞Єќ™£Ї1344+672 ![]() £Ѓ
£Ѓ
”…µ»—ь÷±љ«»эљ«–ќµƒ–‘÷ ЇЌ“—÷™ћхЉюµ√≥цAP1= ![]() £ђAP2=1+
£ђAP2=1+ ![]() £ђAP3=2+
£ђAP3=2+ ![]() £їAP4=2+2
£їAP4=2+2 ![]() £їAP5=3+2
£їAP5=3+2 ![]() £їAP6=4+2
£їAP6=4+2 ![]() £їAP7=4+3
£їAP7=4+3 ![]() £їAP8=5+3
£їAP8=5+3 ![]() £їAP9=6+3
£їAP9=6+3 ![]() £ї√њ»эЄц“ї„й£ђ”…”Џ2013=3°Ѕ671£ђµ√≥цAP2013 £ђ Љіњ…µ√≥цљбєы£Ѓ
£ї√њ»эЄц“ї„й£ђ”…”Џ2013=3°Ѕ671£ђµ√≥цAP2013 £ђ Љіњ…µ√≥цљбєы£Ѓ

 ‘ƒґЅњм≥µѕµЅ–ір∞Є
‘ƒґЅњм≥µѕµЅ–ір∞Є