题目内容
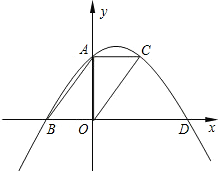 如图,已知平行四边形ABOC的顶点A、B、C在二次函数y=ax2+bx+c的图象上,又点A、B分别在y轴和x轴上,∠ABO=45°.图象顶点的横坐标为2,求二次函数解析式.
如图,已知平行四边形ABOC的顶点A、B、C在二次函数y=ax2+bx+c的图象上,又点A、B分别在y轴和x轴上,∠ABO=45°.图象顶点的横坐标为2,求二次函数解析式.
分析:由已知图象顶点的横坐标为2,即对称轴x=2,AC∥x轴,根据抛物线的对称性可知AC=BO=4,又∠ABO=45°,故AO=BO=4,可推出A(0,4),B(-4,0),由对称性得D(8,0),可设交点式求二次函数解析式.
解答:解:由已知得抛物线对称轴为x=2,
∵AC∥x轴,ABOC为平行四边形,
∴根据抛物线的对称性得AC=BO=4,
又∵在Rt△AOB中,∠ABO=45°,
∴AO=BO=4,
∴A(0,4),B(-4,0),由对称性得D(8,0),
设抛物线解析式为y=a(x+4)(x-8),将A(0,4)代入,
得-32a=4,解得a=-
,
∴y=-
(x+4)(x-8),即y=-
x2+
x+4.
∵AC∥x轴,ABOC为平行四边形,
∴根据抛物线的对称性得AC=BO=4,
又∵在Rt△AOB中,∠ABO=45°,
∴AO=BO=4,
∴A(0,4),B(-4,0),由对称性得D(8,0),
设抛物线解析式为y=a(x+4)(x-8),将A(0,4)代入,
得-32a=4,解得a=-
| 1 |
| 8 |
∴y=-
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
点评:本题考查了用待定系数法求二次函数解析式的方法.关键是根据条件确定抛物线解析式的形式,再求其中的待定系数.一般式:y=ax2+bx+c(a≠0);顶点式y=a(x-h)2+k,其中顶点坐标为(h,k);交点式y=a(x-x1)(x-x2),抛物线与x轴两交点为(x1,0),(x2,0).

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
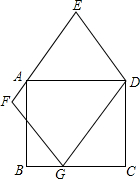 CD的边长a等于点P,Q间的距离.
CD的边长a等于点P,Q间的距离.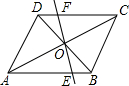 如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.
如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.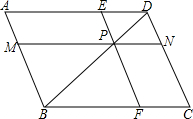 交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF.
交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF. 23、如图,已知平行四边形ABCD.
23、如图,已知平行四边形ABCD.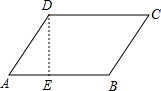 如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.
如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.