题目内容
如图,已知平行四边形DEFG与正方形ABCD有一个公共顶点D,G在CB或其延长线上,A在EF所在直线上,又二次函数y=(m-1)x2-(m-2)x-1(m>0)与x轴的两个交点P、Q的横坐标分别为x1,x2,且x1>0,x2>0,正方形AB CD的边长a等于点P,Q间的距离.
CD的边长a等于点P,Q间的距离.(1)求m的取值范围;
(2)求a和四边形DEFG的面积S;
(3)若DEFG的一组邻边长分别等于x1,x2,并设
| CG | CB |
((2),(3)的结果都用含m的代数式表示)
分析:(1)由于x1,x2均为正数因此x1•x2>0,由此可求出m的取值范围;
(2)可根据抛物线的解析式求出x1,x2的值,即可得出PQ的距离即a的值,求四边形DEFG的面积就要知道底边和高的值,可过A作CD的垂线设垂足为M,那么不难得出△ADM∽△DGC,由此可证得GD•AM的值正好是正方形边长的平方,即平行四边形的面积和正方形的面积相等,由此可求出S的值;
(3)求sin∠E可通过构建直角三角形来解,过D作DN⊥EF于N,那么在直角三角形DEN中,sin∠E=
,而DN可用正方形的面积
除以EF求得,因此∠E的正弦值就等于正方形的面积(即平行四边形的面积)除以EF与DE的积,正方形的面积已经求得,而DE与
EF的积可在(2)也可得出,据此可求出∠E的正弦值,可根据CG和CB的比例关系,用k表示出CG的长,然后在直角三角形CGD中,用勾股定理即可求出k的值.
(2)可根据抛物线的解析式求出x1,x2的值,即可得出PQ的距离即a的值,求四边形DEFG的面积就要知道底边和高的值,可过A作CD的垂线设垂足为M,那么不难得出△ADM∽△DGC,由此可证得GD•AM的值正好是正方形边长的平方,即平行四边形的面积和正方形的面积相等,由此可求出S的值;
(3)求sin∠E可通过构建直角三角形来解,过D作DN⊥EF于N,那么在直角三角形DEN中,sin∠E=
| DN |
| DE |
除以EF求得,因此∠E的正弦值就等于正方形的面积(即平行四边形的面积)除以EF与DE的积,正方形的面积已经求得,而DE与
EF的积可在(2)也可得出,据此可求出∠E的正弦值,可根据CG和CB的比例关系,用k表示出CG的长,然后在直角三角形CGD中,用勾股定理即可求出k的值.
解答: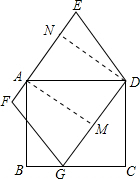 解:(1)∵二次函数y=(m-1)x2-(m-2)x-1(m>0)与x轴的两个交点,
解:(1)∵二次函数y=(m-1)x2-(m-2)x-1(m>0)与x轴的两个交点,
P、Q的横坐标分别为x1,x2,且x1>0,x2>0,
∴x1•x2=-
>0,
解得m<1,
又∵m>0,
∴0<m<1;
(2)令抛物线中y=0,可得0=(m-1)x2-(m-2)x-1,
解得x=1或x=
,
∵0<m<1,
∴
>1,
∴a=
-1=
,
过A作AM⊥GD于M,则有△AMD∽△DCG,
∴
=
,
即AM•GD=a2,
∴S=AM•GD=a2=(
)2=
;
(3)过D作DN⊥EF于N,则sin∠E=
,
∵S=EF•DN=a2,
∴DN=
,即sin∠E=
=
=
,
∵
=k,
∴CG=BC•k=
,
当DG=1时,在直角三角形CDG中,DG2=DC2+CG2,
即1=(
)2+(
)2,
解得k=
,
当0<m<
时,k=
,
当
<m<1时,k=
,
当DG=
时,同理可求得k=
,
∴k的值为
或
.
 解:(1)∵二次函数y=(m-1)x2-(m-2)x-1(m>0)与x轴的两个交点,
解:(1)∵二次函数y=(m-1)x2-(m-2)x-1(m>0)与x轴的两个交点,P、Q的横坐标分别为x1,x2,且x1>0,x2>0,
∴x1•x2=-
| 1 |
| m-1 |
解得m<1,
又∵m>0,
∴0<m<1;
(2)令抛物线中y=0,可得0=(m-1)x2-(m-2)x-1,
解得x=1或x=
| 1 |
| 1-m |
∵0<m<1,
∴
| 1 |
| 1-m |
∴a=
| 1 |
| 1-m |
| m |
| 1-m |
过A作AM⊥GD于M,则有△AMD∽△DCG,
∴
| AM |
| CD |
| AD |
| DG |
即AM•GD=a2,
∴S=AM•GD=a2=(
| m |
| 1-m |
| m2 |
| m2-2m+1 |
(3)过D作DN⊥EF于N,则sin∠E=
| DN |
| DE |
∵S=EF•DN=a2,
∴DN=
| a2 |
| EF |
| a2 |
| DE•EF |
(
| ||
|
| m2 |
| 1-m |
∵
| CG |
| BC |
∴CG=BC•k=
| mk |
| 1-m |
当DG=1时,在直角三角形CDG中,DG2=DC2+CG2,
即1=(
| m |
| 1-m |
| km |
| 1-m |
解得k=
| ||
| m |
当0<m<
| 1 |
| 2 |
| ||
| m |
当
| 1 |
| 2 |
| ||
| m |
当DG=
| 1 |
| 1-m |
| ||
| m |
∴k的值为
| ||
| m |
| ||
| m |
点评:本题考查了平行四边形和正方形的性质、图形面积的求法以及二次函数的应用等知识.综合性强,难度较大.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.
如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.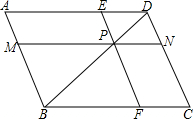 交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF.
交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF. 23、如图,已知平行四边形ABCD.
23、如图,已知平行四边形ABCD. 如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.
如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.