题目内容
如图，已知平行四边形ABCD中，P是对角线BD上的一点，过P点作MN∥AD，EF∥CD，分别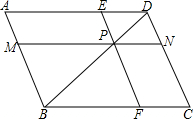
交AB、CD、AD、BC于M、N、E、F，设a=PM•PE，b=PN•PF．（1）请判断a与b的大小关系，并说明理由；
（2）当
| BP |
| PD |
| S平行四边形PEAM |
| S△ABD |
分析：（1）根据AD∥BC，可求出△PDE∽△PBF，因此PD：PB=PE：PF．同理可在相似三角形△PDN和△PBM中，求得PD：PB=PN：PM，两个比例关系式的等值替换，即可求出PM•PE=PN•FP，即a=b；
（2）根据PM∥AD，可求出△BPM∽△ABD，可得出△PMB和△ABD的面积比；同理可求出△PED和△ABD的面积比．由于四边形AMPE的面积为△ABD、△PMB、△PED的面积差，由此可求出平行四边形PEAM与△ABD的面积比．
（2）根据PM∥AD，可求出△BPM∽△ABD，可得出△PMB和△ABD的面积比；同理可求出△PED和△ABD的面积比．由于四边形AMPE的面积为△ABD、△PMB、△PED的面积差，由此可求出平行四边形PEAM与△ABD的面积比．
解答：解：（1）a=b
理由：∵BC∥AD
∴△PDE∽△PBF
∴
=
∵AB∥CD
∴△PDN∽△PBM
∴
=
∴
=
∴PM•PE=PN•PF
∴a=b；
（2）∵
=2
∴
=
，
∵MN∥AD，EF∥CD，
∴四边形BFPM是平行四边形
∴△PBF≌△BPM
∴
=
=
，
∴S△BPM=4S△PDE
∵
=2
∴
=
∴
=
，
∴S△BPM=
S△BDA，
∵S△PDE=
S△BPM=
S△BDA，
∴S四边形PEAM=
S△BDA
∴
=
．
理由：∵BC∥AD
∴△PDE∽△PBF
∴
| PE |
| PF |
| PD |
| PB |
∵AB∥CD
∴△PDN∽△PBM
∴
| PN |
| PM |
| PD |
| PB |
∴
| PE |
| PF |
| PN |
| PM |
∴PM•PE=PN•PF
∴a=b；
（2）∵
| BP |
| PD |
∴
| S△PBF |
| S△PDE |
| 4 |
| 1 |
∵MN∥AD，EF∥CD，
∴四边形BFPM是平行四边形
∴△PBF≌△BPM
∴
| S△BPM |
| S△PDE |
| S△PBF |
| S△PDE |
| 4 |
| 1 |
∴S△BPM=4S△PDE
∵
| BP |
| PD |
∴
| BP |
| BD |
| 2 |
| 3 |
∴
| S△BPM |
| S△BDA |
| 4 |
| 9 |
∴S△BPM=
| 4 |
| 9 |
∵S△PDE=
| 1 |
| 4 |
| 1 |
| 9 |
∴S四边形PEAM=
| 4 |
| 9 |
∴
| S平行四边形PEAM |
| S△ABD |
| 4 |
| 9 |
点评：本题主要考查了平行四边形的性质、相似三角形的判定和性质等知识．综合性强，难度较大．
练习册系列答案
相关题目
CD的边长a等于点P，Q间的距离．
如图，已知平行四边形ABCD的对角线AC，BD相交于点O，BD绕点O顺时针旋转交AB，DC于E，F．
23、如图，已知平行四边形ABCD．
如图，已知平行四边形ABCD，作DE⊥AB，垂足为E，把三角形AED沿AB方向平移AB长个单位长度．