题目内容
如图，已知平行四边形ABCD的对角线AC，BD相交于点O，BD绕点O顺时针旋转交AB，DC于E，F．（1）证明：四边形BFDE是平行四边形；
（2）BD绕点O顺时针旋转
分析：（1）易证△DOF≌△BOE，那么OF=OE，所以利用对角线相等的四边形是平行四边形即可求证．
（2）只需让对角线互相垂直即可．
（2）只需让对角线互相垂直即可．
解答：（1）证明：∵四边形ABCD是平行四边形，
∴OB=OD，AB∥CD，（2分）
∴∠OBE=∠ODF，（3分）
又∠BOE=∠DOF，（4分）
∴△BOE≌△DOF，（5分）
∴OE=OF且OB=OD，
∴四边形BFDE是平行四边形．（6分）
（2）解：BD绕点O顺时针旋转90度时，平行四边形BFDE是菱形．（7分）
证明：∵四边形BFDE是平行四边形，
又∠DOF=90°，
∴FE⊥BD，（8分）
∴平行四边形BFDE是菱形．（9分）
∴OB=OD，AB∥CD，（2分）
∴∠OBE=∠ODF，（3分）
又∠BOE=∠DOF，（4分）
∴△BOE≌△DOF，（5分）
∴OE=OF且OB=OD，
∴四边形BFDE是平行四边形．（6分）
（2）解：BD绕点O顺时针旋转90度时，平行四边形BFDE是菱形．（7分）
证明：∵四边形BFDE是平行四边形，
又∠DOF=90°，
∴FE⊥BD，（8分）
∴平行四边形BFDE是菱形．（9分）
点评：出现上图时，通常要证新直线所在的三角形全等，注意菱形和对角线相关的判定．
练习册系列答案
相关题目
CD的边长a等于点P，Q间的距离．
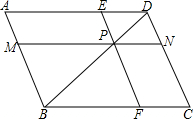交AB、CD、AD、BC于M、N、E、F，设a=PM•PE，b=PN•PF．
23、如图，已知平行四边形ABCD．
如图，已知平行四边形ABCD，作DE⊥AB，垂足为E，把三角形AED沿AB方向平移AB长个单位长度．