题目内容
直线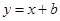 与
与 轴交于点C(4,0),与
轴交于点C(4,0),与 轴交于点B,并与双曲线
轴交于点B,并与双曲线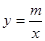
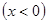 交于点
交于点 。
。
(1)求直线与双曲线的解析式。
(2)连接OA,求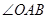 的正弦值。
的正弦值。
(3)若点D在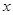 轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。
轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。
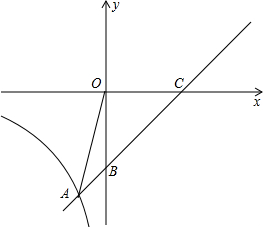
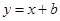 与
与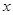 轴交于点C(4,0),与
轴交于点C(4,0),与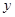 轴交于点B,并与双曲线
轴交于点B,并与双曲线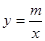
 交于点
交于点 。
。(1)求直线与双曲线的解析式。
(2)连接OA,求
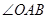 的正弦值。
的正弦值。(3)若点D在
 轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。
轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。
(1) y=x-4; ;(2)
;(2) 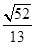 ;(3) (6,0)或(20,0).
;(3) (6,0)或(20,0).
 ;(2)
;(2) 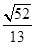 ;(3) (6,0)或(20,0).
;(3) (6,0)或(20,0).试题分析:(1)把点C的坐标代入y=x+b,求出b的值,得出直线的解析式;把点A(-1,n)代入y=x-4得到n的值,求出A点的坐标,再把将A点代入
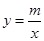 (x<0)中,求出m的值,从而得出双曲线的解析式;
(x<0)中,求出m的值,从而得出双曲线的解析式;(2)先过点O作OM⊥AC于点M,根据B点经过y轴,求出B点的坐标,根据勾股定理求出AO的值,根据OC=OB=4,得出△OCB是等腰三角形,求出∠OBC=∠OCB的度数,再在△OMB中,根据正弦定理求出OM的值,从而得出∠OAB的正弦值.
(3)先过点A作AN⊥y轴,垂足为点N,根据AN=1,BN=1,求出AB的值,根据OB=OC=4,求出BC的值,再根据∠OBC=∠OCB=45°,得出∠OBA=∠BCD,从而得出△OBA∽△BCD或△OBA∽△DCB,最后根据
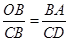 ,再代入求出CD的长,即可得出答案.
,再代入求出CD的长,即可得出答案.试题解析:(1)∵直线y=x+b与x轴交于点C(4,0),
∴把点C(4,0)代入y=x+b得:b=-4,
∴直线的解析式是:y=x-4;
∵直线也过A点,
∴把A点代入y=x-4得到:n="-5"
∴A(-1,-5),
把将A点代入
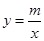 (x<0)得:m=5,
(x<0)得:m=5,∴双曲线的解析式是:
 ;
;(2)过点O作OM⊥AC于点M,
∵B点经过y轴,
∴x=0,
∴0-4=y,
∴y=-4,
∴B(0,-4),
AO=
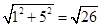 ,
,∵OC=OB=4,
∴△OCB是等腰三角形,
∴∠OBC=∠OCB=45°,
∴在△OMB中 sin45°=
 ,
,∴OM=2
 ,
,∴在△AOM中,
sin∠OAB=
 ;
;(3)存在;
过点A作AN⊥y轴,垂足为点N,
则AN=1,BN=1,
则AB=
 ,
,∵OB=OC=4,
∴BC=
 ,
,∠OBC=∠OCB=45°,
∴∠OBA=∠BCD=135°,
∴△OBA∽△BCD或△OBA∽△DCB,
∴
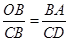 ,
,∴
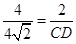 或
或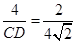 ,
,∴CD=2或CD=16,
∴点D的坐标是(6,0)或(20,0).

练习册系列答案
相关题目
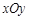 中,正方形
中,正方形 的边长为2.写出一个函数
的边长为2.写出一个函数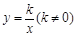 ,使它的图象与正方形
,使它的图象与正方形
 的图象上有两点
的图象上有两点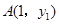 ,
,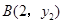 ,则
,则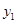 ______
______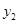 (填“
(填“ ”或“
”或“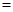 ”或“
”或“ ”).
”).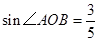 ,反比例函数
,反比例函数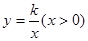 的图象经过AO的中点C,且与AB交于点D,则BD = .
的图象经过AO的中点C,且与AB交于点D,则BD = .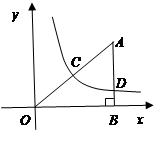
 (x>0)图象上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B.则△ABC的周长为 .
(x>0)图象上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B.则△ABC的周长为 .
 时,函数值y满足
时,函数值y满足 ,则这个函数可以是( )
,则这个函数可以是( )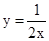

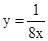

 (x>0)的图象于点B1,B2,B3,…Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn,则S1+S2+S3+…+Sn= .
(x>0)的图象于点B1,B2,B3,…Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn,则S1+S2+S3+…+Sn= .
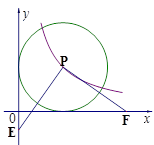
 (x>0)上,以P为圆心的⊙P与两坐标轴都相切,点E为y轴负半轴上的一点,过点P作PF⊥PE交x轴于点F,若OF-OE=6,则k的值是 .
(x>0)上,以P为圆心的⊙P与两坐标轴都相切,点E为y轴负半轴上的一点,过点P作PF⊥PE交x轴于点F,若OF-OE=6,则k的值是 .