题目内容
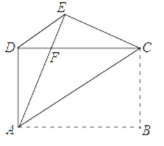
【题目】如图,在长方形ABCD中,AB>BC,把长方形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE
求证:(1)△AED≌△CDE
(2)△EFD是等腰三角形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据矩形的性质可得出AD=BC、AB=CD,结合折叠的性质可得出AD=CE、AE=CD,进而即可证出△ADE≌△CED(SSS);
(2)根据全等三角形的性质可得出∠DEF=∠EDF,利用等边对等角可得出EF=DF,由此即可证出△DEF是等腰三角形.
证明:(1)∵四边形ABCD是矩形,
∴AD=BC,AB=CD.
由折叠的性质可得:BC=CE,AB=AE,
∴AD=CE,AE=CD.
在△ADE和△CED中,
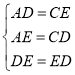 ,
,
∴△ADE≌△CED(SSS).
(2)由(1)得△ADE≌△CED,
∴∠DEA=∠EDC,即∠DEF=∠EDF,
∴EF=DF,
∴△DEF是等腰三角形.

练习册系列答案
相关题目