题目内容
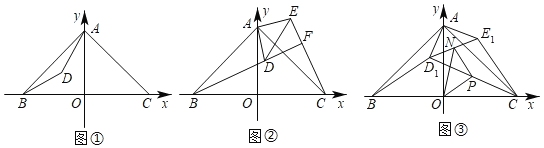
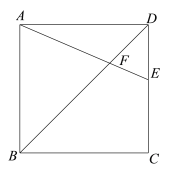
【题目】在正方形ABCD中,E是CD边上一点(CE>DE),AE,BD交于点F.
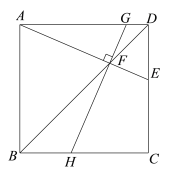
(1)如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.
求证:∠EAB=∠GHC;
(2)AE的垂直平分线分别与AD,AE,BD交于点P,M,N,连接CN.
①依题意补全图形;
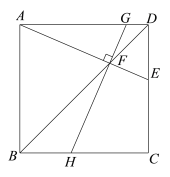

图1 备用图
②用等式表示线段AE与CN之间的数量关系,并证明.
【答案】(1)详见解析;(2)①补全图形,如图所示.②![]() .详见解析
.详见解析
【解析】
(1)根据正方形的性质,有AD∥BC,∠BAD=90°,得到∠AGH=∠GHC,再根据GH⊥AE,得到∠EAB=∠AGH,即可证明.
(2)①根据垂直平分线的作法步骤进行即可.
②连接AN,连接EN并延长,交AB边于点Q,根据正方形的性质,得到NA=NC,∠1=∠2,再根据垂直平分线的性质,得到NA=NE,进而得到NC=NE,∠3=∠4,在正方形ABCD中,BA∥CE,∠BCD=90°,得到∠AQE=∠4,∠1+∠AQE=∠2+∠3=90°,∠ANE=∠ANQ=90°,最后在Rt△ANE中,即可求解.
(1)证明:在正方形ABCD中,AD∥BC,∠BAD=90°,
∴∠AGH=∠GHC.
∵GH⊥AE,
∴∠EAB=∠AGH.
∴∠EAB=∠GHC.
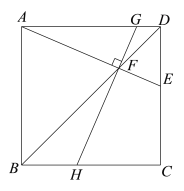
(2)①补全图形,如图所示.
②![]() .
.
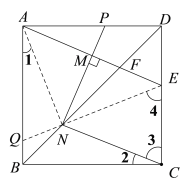
证明:连接AN,连接EN并延长,交AB边于点Q.
∵四边形ABCD是正方形,
∴点A,点C关于BD对称.
∴NA=NC,∠1=∠2.
∵PN垂直平分AE,
∴NA=NE.
∴NC=NE.
∴∠3=∠4.
在正方形ABCD中,BA∥CE,∠BCD=90°,
∴∠AQE=∠4.
∴∠1+∠AQE=∠2+∠3=90°.
∴∠ANE=∠ANQ=90°.
在Rt△ANE中,
∴![]() .
.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案【题目】市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班,为了解学生对这四类兴趣班的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表

兴趣班 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
| |
合计 |
|
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() _____,
_____,![]() ;
;
(2)根据调查结果,请你估计该市![]() 名小学生中最喜欢“绘画”兴趣班的人数;
名小学生中最喜欢“绘画”兴趣班的人数;
(3)王强和李昊选择参加兴趣班,若王强从![]() 三类兴趣班中随机选取一类,李吴从
三类兴趣班中随机选取一类,李吴从![]() 三类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类兴趣班的概率.
三类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类兴趣班的概率.