题目内容
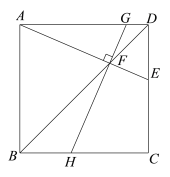
【题目】如图,在平面直角坐标系中,O为原点,点A(0,4),B(﹣4,0),C(4,0).
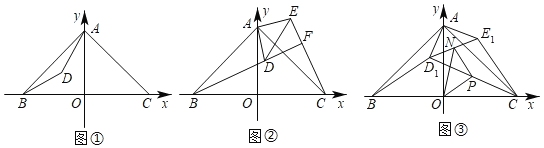
(1)如图①,若∠BAD=15°,AD=3,求点D的坐标;
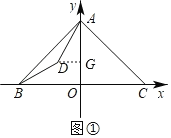
(2)如图②,AD=2,将△ABD绕点A逆时针方向旋转得到△ACE,点B,D的对应点分别为C,E.连接DE,BD的延长线与CE相交于点F.
①求DE的长;
②证明:BF⊥CE.
(3)如图③,将(2)中的△ADE绕点A在平面内旋转一周,在旋转过程中点D,E的对应点分别为D1,E1,点N,P分别为D1E1,D1C的中点,请直接写出△OPN面积S的变化范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②见解析;(3)
;②见解析;(3)![]()
【解析】
(1)如图①中,过点D作DG⊥OA,垂足为G.解直角三角形求出DG,OG即可.
(2)①利用勾股定理求出即可.
②证明△ABD≌△ACE(SAS),可得结论.
(3)证明△OPN是等腰直角三角形,求出OP的取值范围,求出△OPN的面积的最小值以及最大值即可.
解:(1)∵OA=OB=4,∠AOB=90°,
∴∠OAB=∠ABO=45°.
∴∠DAO=∠OAB﹣∠DAB=30°.
如图①中,过点D作DG⊥OA,垂足为G.
在Rt△ADG中,∠DAG=30°,
∴![]() ,
,![]()
∴![]() .
.
∴点D的坐标为![]() .
.
(2)①如图②中,
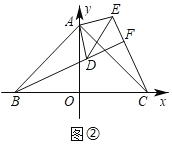
∵∠DAE=∠BAC=90°,AD=AE=2,
∴在![]() 中,
中,![]() .
.
②∵OA=OB=OC=4,∠AOB=∠AOC=90°,
∴∠OAB=∠ABO=∠ACO=∠OAC=45°,
∴∠BAC=90°,
∵△ABD旋转得到△ACE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
在△BFC中,则有∠FBC+∠FCB=∠FBC+∠BCA+∠ACE=∠FBC+∠BCA+∠ABD=∠ABC+∠BCA=90°,
∴BF⊥CE.
(3)如图③中,

∵OB=OC,PC=PD1,NE1=ND1,
∴OP=![]() BD1,PN=
BD1,PN=![]() E1C,OP∥BD1,PN∥CE1
E1C,OP∥BD1,PN∥CE1
∵BD1⊥E1C,BD1=E1C,
∴OP⊥PN,OP=PN,
∴△OPN是等腰直角三角形,
∵AB=4![]() ,AD1=2,
,AD1=2,
∴4![]() ﹣2≤BD1≤4
﹣2≤BD1≤4![]() +2,
+2,
∴2![]() ﹣1≤OP≤2
﹣1≤OP≤2![]() +1,
+1,
∴△OPN面积的最小值=![]() (2
(2![]() ﹣1)2=
﹣1)2=![]() ﹣2
﹣2![]() ,△OPN的面积的最大值=
,△OPN的面积的最大值=![]() +2
+2![]() ,
,
∴![]() .
.

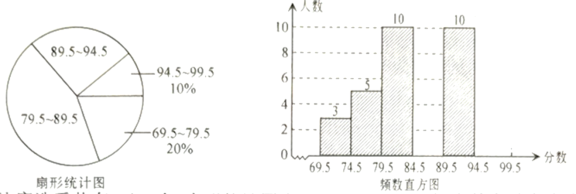
【题目】为了解某地区企业信息化发展水平,从该地区中随机抽取50家企业调研,针对体现企业信息化发展水平的A和B两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A项指标成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
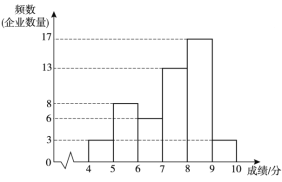
b.A项指标成绩在![]() 这一组的是:
这一组的是:
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c.![]() 两项指标成绩的平均数、中位数、众数如下:
两项指标成绩的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
A项指标成绩 | 7.37 | m | 8.2 |
B项指标成绩 | 7.21 | 7.3 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m的值
(2)在此次调研评估中,某企业A项指标成绩和B项指标成绩都是7.5分,该企业成绩排名更靠前的指标是______________(填“A”或“B”),理由是_____________;
(3)如果该地区有500家企业,估计A项指标成绩超过7.68分的企业数量.