题目内容
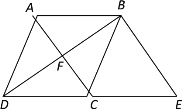
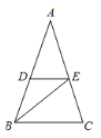
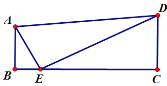
【题目】如图,四边形ABCD中,∠ABC=∠BCD=90°,点E在BC边上,∠AED=90°
(1)求证:∠BAE=∠CED;(2)若AB+CD=DE,求证:AE+BE=CE
(3)在(2)的条件下,若△CDE与△ABE的面积的差为18,CD=6,求BE的长.


【答案】(1)见解析;(2)见解析;(3)3.
【解析】
(1)由∠AEB+∠CED=180°90°=90°,∠BAE+∠AEB=90°,即可得出结论;
(2)在ED上截取EF=AB,过点F作FG⊥DE交BC于G,连接DG,证出∠BAE=∠FEG,由ASA证得△ABE≌△EFG得出AE=EG,BE=FG,由AB+CD=DE,EF+DF=DE,得出DF=CD,由HL证得Rt△DFG≌Rt△DCG得出FG=CG,则BE=CG,即可得出结论;
(3)由△ABE≌△EFG,Rt△DFG≌Rt△DCG,得出S△ABE=S△EFG,S△DFG=S△DCG,则S△CDES△ABE=2S△CDG=18,得出S△CDG=9,则![]() CGCD=9,即可得出结果.
CGCD=9,即可得出结果.
(1)证明:∵∠AEB+∠CED=180°90°=90°,∠BAE+∠AEB=90°,
∴∠BAE=∠CED;
(2)证明:在ED上截取EF=AB,过点F作FG⊥DE交BC于G,连接DG,如图所示:
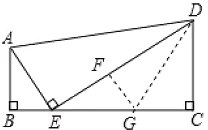
∵∠AEB+∠GEF=90°,∠BAE+∠AEB=90°,
∴∠BAE=∠FEG,
在△ABE和△EFG中,
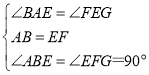 ,
,
∴△ABE≌△EFG(ASA),
∴AE=EG,BE=FG,
∵AB+CD=DE,EF+DF=DE,
∴DF=CD,
在Rt△DFG和Rt△DCG中,
![]() ,
,
∴Rt△DFG≌Rt△DCG(HL),
∴FG=CG,
∴BE=CG,
∴AE+BE=EG+CG=CE;
(3)解:∵△ABE≌△EFG,Rt△DFG≌Rt△DCG,
∴S△ABE=S△EFG,S△DFG=S△DCG,
∴S△CDES△ABE=2S△CDG=18,
∴S△CDG=9,
∴![]() CGCD=9,即
CGCD=9,即![]() ×CG×6=9,
×CG×6=9,
∴CG=BE=3.

 阅读快车系列答案
阅读快车系列答案