题目内容
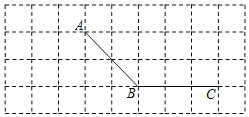
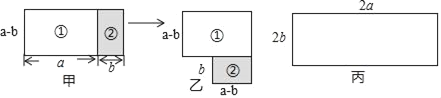
【题目】如图所示,图甲由长方形①,长方形②组成,图甲通过移动长方形②得到图乙.
(1)S甲= ,S乙= (用含a、b的代数式分别表示);
(2)利用(1)的结果,说明a2、b2、(a+b)(a﹣b)的等量关系;
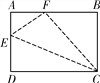
(3)现有一块如图丙尺寸的长方形纸片,请通过对它分割,再对分割的各部分移动,组成新的图形,画出图形,利用图形说明(a+b)2、(a﹣b)2、ab三者的等量关系.
【答案】(1)(a+b)(ab);a2b2;(2)(a+b)(ab)=a2b2;(3)见解析
【解析】
(1)根据长方形的面积计算公式以及正方形的面积计算公式进行计算,即可得到结论;
(2)根据S甲=S乙即可得到a2、b2、(a+b)(ab)的等量关系;
(3)将图丙分成四个长为a,宽为b的小长方形,再拼成大正方形,即可得到(a+b)2、(a﹣b)2、ab三者的等量关系.
解:(1)由题可得,S甲=(a+b)(ab);
S乙=a2b2;
故答案为:(a+b)(ab);a2b2;
(2)∵S甲=S乙;
∴a2、b2、(a+b)(ab)的等量关系为:(a+b)(ab)=a2b2;
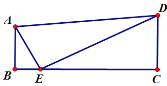
(3)如图①所示,将图丙分成四个长为a,宽为b的小长方形,再拼成如图②所示的正方形.
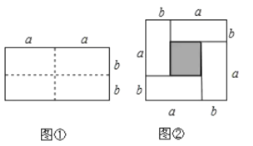
根据图②可得:
S大正方形=(a+b)2,
S大正方形=(ab)2+4ab,
∴(a+b)2=(ab)2+4ab.

练习册系列答案
相关题目