题目内容
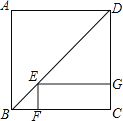
【题目】如图,在四边形ABCD中,AB∥CD,AC垂直平分BD,交BD于点F,延长DC到点E,使得CE=DC,连接BE.
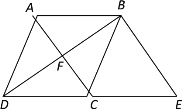
(1)求证:四边形ABCD是菱形.
(2)填空:
①当∠ADC= °时,四边形ACEB为菱形;
②当∠ADC=90°,BE=4时,则DE=
【答案】(1)见解析;(2)①60 ;②![]() .
.
【解析】
(1)由“有一组对边平行且相等的四边形是平行四边形”证得四边形ABCD为平行四边形,再由“邻边相等的平行四边形是菱形”证得四边形ABCD是菱形.
(2)①由“有一组对边平行且相等的四边形是平行四边形”证得四边形ABEC为平行四边形,再由“邻边相等的平行四边形是菱形”证得四边形ABEC是菱形,则CA=AD=DC,此时三角形ADC为等边三角形,∠ADC=60°;②当∠ADC=90°时,四边形ABCD为正方形,三角形BCE为等腰直角三角形,因为BE=4,所以由勾股定理得CE=![]() ,
,![]() .
.
解:(1)证明:∵AC垂直平分BD,∴AB=AD ,BF=DF,
∵AB∥CD,∴∠ABD=∠CDB.
∵∠AFB=∠CFD,∴△AFB≌△CFD (ASA),
∴AB=CD.又∵AB∥CD,∴四边形ABCD是平行四边形 .
∵AB=AD,∴平行四边形ABCD是菱形 .
(2)①∵由(1)得:四边形ABCD是菱形,
∴AB=CD,AB//CD,
∵CE是CD的延长线,且CE=CD,
∴由“有一组对边平行且相等的四边形是平行四边形”证得四边形ABEC为平行四边形
∵假设四边形ACEB为菱形,∴AC=CE
∵已知AD=DC,∴AC=DC=AD,即三角形ADC为等边三角形,∴![]()
②∵由(1)得:四边形ABCD是菱形,且∠ADC=90°
∴四边形ABCD为正方形,三角形BCE为直角三角形,
∵CE=CD,∴由勾股定理得CE=![]() ,
,![]() .
.

 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案