题目内容
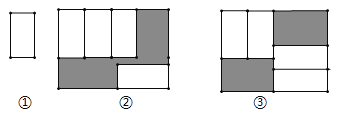
【题目】把四张大小相同的长方形卡片（如图①）按图②、图③两种放法放在一个底面为长方形（长为
，宽为
）的盒底上，底面未被卡片覆盖的部分用阴影表示，若记图②中阴影部分的周长为
，图③中阴影部分的周长为
，则
___________.
【答案】2m-2n.
【解析】
此题要先设小长方形的长为acm，宽为bcm，再结合图形得出2b+a=m，分别表示图形②的阴影周长和图形③的阴影周长，作差后即可求出答案.
解：设小长方形的长为a，宽为b， 由图可知2b+a=m，
∴②阴影部分的周长为：
=2（m+n），
∴③阴影部分的周长为：
=2m+2（n-a）+2（n-2b）=2m+4n-2(2b+a)= 2m+4n-2m=4n,
∴C2-C3=2（m+n）-4n=2m-2n.
故答案为2m-2n.
练习册系列答案
应用题作业本系列答案
相关题目
