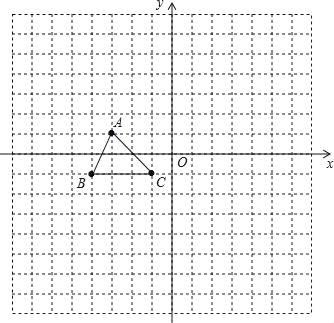
[题目]如图.点A.B.C的坐标分别为(﹣3.1)..(﹣1.﹣1).将△ABC先向下平移2个单位.得△A1B1C1,再将△A1B1C1沿y轴翻折180°.得△A2B2C2,．(1)画出△A1B1C1和△A2B2C2,(2)求直线A2A的解析式．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，点A、B、C的坐标分别为（﹣3，1）、（﹣4，﹣1）、（﹣1，﹣1），将△ABC先向下平移2个单位，得△A1B1C1；再将△A1B1C1沿y轴翻折180°，得△A2B2C2；．

（1）画出△A1B1C1和△A2B2C2；

（2）求直线A2A的解析式．

【答案】（1）见解析；（2）

【解析】分析：（1）将△ABC的三个顶点分别向下平移2个单位，得到新的对应点，顺次连接得△A1B1C1；再从△A1B1C1三个顶点向y轴引垂线并延长相同单位，得到新的对应点，顺次连接，得△A2B2C2；

（2）设直线A2A的解析式为y=kx+b，再把点A（﹣3，1），A2（3，﹣1）代入，用待定系数法求出它的解析式．

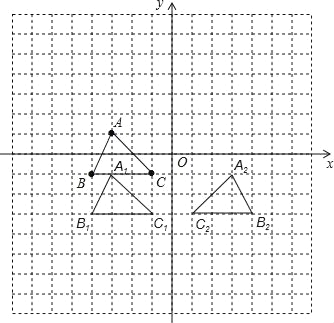
详解：（1）如图所示：△A1B1C1，△A2B2C2即为所求；

（2）设直线A2A的解析式为y=kx+b

把点的坐标A（﹣3，1）A2的坐标（3，﹣1）代入上式得：

，

解得：，

所以直线A2A的解析式为．

练习册系列答案

相关题目

【题目】如图，已知线段，点是线段的中点，先按要求画图形，再解决问题．

（1）延长线段至点，使；延长线段至点，使；（尺规作图，保留作图痕迹）

（2）求线段的长度；

（3）若点是线段的中点，求线段的长度．

【题目】平面直角坐标系中，直线l1:与x轴交于点A，与y轴交于点B，直线l2:与x轴交于点C，与直线l1交于点P．

（1）当k=1时，求点P的坐标；

（2）如图1，点D为PA的中点，过点D作DE⊥x轴于E，交直线l2于点F，若DF=2DE，求k的值；

（3）如图2，点P在第二象限内，PM⊥x轴于M，以PM为边向左作正方形PMNQ，NQ的延长线交直线l1于点R，若PR=PC，求点P的坐标．

【题目】某周日上午8：00小宇从家出发，乘车1小时到达某活动中心参加实践活动．11：00时他在活动中心接到爸爸的电话，因急事要求他在12：00前回到家，他即刻按照来活动中心时的路线，以5千米/小时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家x（小时）后，到达离家y（千米）的地方，图中折线OABCD表示y与x之间的函数关系．

（1）活动中心与小宇家相距千米，小宇在活动中心活动时间为小时，他从活动中心返家时，步行用了小时；

（2）求线段BC所表示的y（千米）与x（小时）之间的函数关系式（不必写出x所表示的范围）；

（3）根据上述情况（不考虑其他因素），请判断小宇是否能在12：00前回到家，并说明理由．

【题目】如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（，0），B（0，2），则B2的坐标为_____；点B2016的坐标为_____．