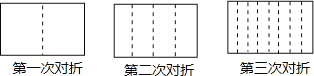
ЬтФПФкШн
ЁОЬтФПЁПвбжЊЪ§жсЩЯСНЕу![]() ЁЂ
ЁЂ![]() ЖдгІЕФЪ§ЗжБ№ЪЧ-1ЃЌ3ЃЌЕу
ЖдгІЕФЪ§ЗжБ№ЪЧ-1ЃЌ3ЃЌЕу![]() ЮЊЪ§жсЩЯвЛЖЏЕуЃЌвбжЊЪ§жсЩЯСНЕу
ЮЊЪ§жсЩЯвЛЖЏЕуЃЌвбжЊЪ§жсЩЯСНЕу![]() ЁЂ
ЁЂ![]() ЖдгІЕФЪ§ЗжБ№ЮЊ-1ЁЂ3ЃЌЕу
ЖдгІЕФЪ§ЗжБ№ЮЊ-1ЁЂ3ЃЌЕу![]() ЮЊЪ§жсЩЯвЛЖЏЕуЃЌЦфЖдгІЕФЪ§ЮЊ
ЮЊЪ§жсЩЯвЛЖЏЕуЃЌЦфЖдгІЕФЪ§ЮЊ![]() .
.
ЃЈ1ЃЉШєЕу![]() ЕНЕу
ЕНЕу![]() ЃЌЕу
ЃЌЕу![]() ЕФОрРыЯрЕШЃЌЧѓЕу
ЕФОрРыЯрЕШЃЌЧѓЕу![]() ЖдгІЕФЪ§ЃЛ
ЖдгІЕФЪ§ЃЛ
ЃЈ2ЃЉЪ§жсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕу
ЃЌЪЙЕу![]() ЕНЕу
ЕНЕу![]() ЁЂЕу
ЁЂЕу![]() ЕФОрРыжЎКЭЮЊ6ЃПШєДцдкЃЌЧыЧѓГі
ЕФОрРыжЎКЭЮЊ6ЃПШєДцдкЃЌЧыЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕу![]() ЁЂЕу
ЁЂЕу![]() ЗжБ№вд2ИіЕЅЮЛГЄЖШ/ЗжЁЂ1ИіЕЅЮЛГЄЖШ/ЗжЕФЫйЖШЯђгвдЫЖЏЃЌЭЌЪБЕу
ЗжБ№вд2ИіЕЅЮЛГЄЖШ/ЗжЁЂ1ИіЕЅЮЛГЄЖШ/ЗжЕФЫйЖШЯђгвдЫЖЏЃЌЭЌЪБЕу![]() вд6ИіЕЅЮЛГЄЖШ/ЗжЕФЫйЖШДг
вд6ИіЕЅЮЛГЄЖШ/ЗжЕФЫйЖШДг![]() ЕуЯђзѓдЫЖЏ.ЕБгіЕН
ЕуЯђзѓдЫЖЏ.ЕБгіЕН![]() ЪБЃЌЕу
ЪБЃЌЕу![]() СЂМДвдЭЌбљЕФЫйЖШЯђгвдЫЖЏЃЌВЂВЛЭЃЕиЭљЗЕгкЕу
СЂМДвдЭЌбљЕФЫйЖШЯђгвдЫЖЏЃЌВЂВЛЭЃЕиЭљЗЕгкЕу![]() гыЕу
гыЕу![]() жЎМфЃЌЧѓЕБЕу
жЎМфЃЌЧѓЕБЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌЕу
жиКЯЪБЃЌЕу![]() ЫљОЙ§ЕФзмТЗГЬЪЧЖрЩйЃП
ЫљОЙ§ЕФзмТЗГЬЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉ1ЃЛЃЈ2ЃЉ-2Лђ4ЃЛЃЈ3ЃЉ24.
ЁОНтЮіЁП
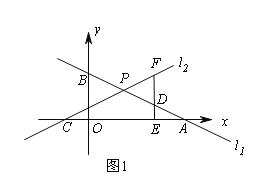
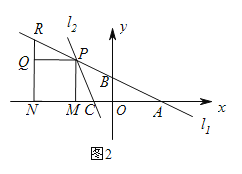
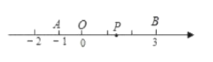
ЃЈ1ЃЉШєЕуPЖдгІЕФЪ§гы-1ЁЂ3ВюЕФОјЖджЕЯрЕШЃЌдђЕуPЕНЕуAЃЌЕуBЕФОрРыЯрЕШЃЛ
ЃЈ2ЃЉИљОнЕБPдкAЕФзѓВрвдМАЕБPдкAЕФгвВрЗжБ№СаГіЗНГЬЧѓГіМДПЩЃЛ
ЃЈ3ЃЉЩшОЙ§aЗжжгЕуAгыЕуBжиКЯЃЌИљОнЕуAБШЕуBдЫЖЏЕФОрРыЖр4ЃЌСаГіЗНГЬЃЌЧѓГіaЕФжЕЃЌМДЮЊЕуPдЫЖЏЕФЪБМфЃЌдйГЫвдЕуPдЫЖЏЕФЫйЖШЃЌПЩЕУЕуPОЙ§ЕФТЗГЬЃЎ
ЃЈ1ЃЉЁпЕу![]() дк
дк![]() ЁЂ
ЁЂ![]() жЎМфЃЌ
жЎМфЃЌ
Ёр![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() дк
дк![]() жЎМфЃЌ
жЎМфЃЌ![]() ЃЈВЛПЩФмгаЃЉЃЛ
ЃЈВЛПЩФмгаЃЉЃЛ
ЕБ![]() дк
дк![]() ЕФзѓВрЃЌ
ЕФзѓВрЃЌ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
ЕБ![]() дк
дк![]() ЕФгвВрЃЌ
ЕФгвВрЃЌ![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЫљвдЕу![]() ЕФжЕЮЊ-2Лђ4ЃЛ
ЕФжЕЮЊ-2Лђ4ЃЛ
ЃЈ3ЃЉЩшОЙ§![]() ЗжжгЕу
ЗжжгЕу![]() гыЕу
гыЕу![]() жиКЯЃЌИљОнЬтвтЕУЃК
жиКЯЃЌИљОнЬтвтЕУЃК
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() .
.
ЁрЕу![]() ОЙ§ЕФТЗГЬЮЊ
ОЙ§ЕФТЗГЬЮЊ![]() ЫйЖШ
ЫйЖШ![]() ЪБМф
ЪБМф![]()
ЁрЕу![]() ОЙ§ЕФТЗГЬЮЊ24
ОЙ§ЕФТЗГЬЮЊ24

 ЬьЬьЯђЩЯПкЫуБОЯЕСаД№АИ
ЬьЬьЯђЩЯПкЫуБОЯЕСаД№АИЁОЬтФПЁПФГгЮгОЙнУПФъЯФМОЭЦГіСНжжгЮгОИЖЗбЗНЪНЃЌЗНЪНвЛЃКЯШЙКТђЛсдБжЄЃЌУПеХЛсдБжЄ100дЊЃЌжЛЯоБОШЫЕБФъЪЙгУЃЌЦОжЄгЮгОУПДЮдйИЖЗб5дЊЃЛЗНЪНЖўЃКВЛЙКТђЛсдБжЄЃЌУПДЮгЮгОИЖЗб9дЊЃЎ
ЩшаЁУїМЦЛЎНёФъЯФМОгЮгОДЮЪ§ЮЊxЃЈxЮЊе§ећЪ§ЃЉЃЎ
ЃЈIЃЉИљОнЬтвтЃЌЬюаДЯТБэЃК
гЮгОДЮЪ§ | 10 | 15 | 20 | Ё | x |
ЗНЪНвЛЕФзмЗбгУЃЈдЊЃЉ | 150 | 175 | ______ | Ё | ______ |
ЗНЪНЖўЕФзмЗбгУЃЈдЊЃЉ | 90 | 135 | ______ | Ё | ______ |
ЃЈЂђЃЉШєаЁУїМЦЛЎНёФъЯФМОгЮгОЕФзмЗбгУЮЊ270дЊЃЌбЁдёФФжжИЖЗбЗНЪНЃЌЫћгЮгОЕФДЮЪ§БШНЯЖрЃП
ЃЈЂѓЃЉЕБx>20ЪБЃЌаЁУїбЁдёФФжжИЖЗбЗНЪНИќКЯЫуЃПВЂЫЕУїРэгЩЃЎ