题目内容
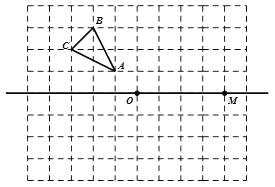
【题目】如图,在平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
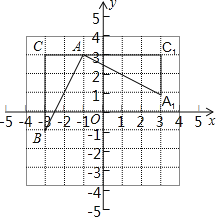
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
(3)设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾股定理.
【答案】(1)O(0,0);90 ;(2)图形详见解析;(3)证明详见解析.
【解析】
试题分析:(1)由图形可知,对应点的连线CC1、AA1的垂直平分线过点O,根据旋转变换的性质,点O即为旋转中心,再根据网格结构,观察可得旋转角为90°;
(2)利用网格结构,分别找出旋转后对应点的位置,然后顺次连接即可;
(3)利用面积,根据正方形CC1C2C3的面积等于正方形AA1A2B的面积加上△ABC的面积的4倍,列式计算即可得证.
试题解析:解:(1)旋转中心坐标是O(0,0),旋转角是90度;
(2)画出的图形如图所示;
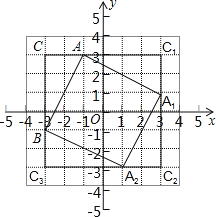
(3)有旋转的过程可知,四边形CC1C2C3和四边形AA1A2B是正方形.
∵S正方形CC1C2C3=S正方形AA1A2B+4S△ABC,
∴(a+b)2=c2+4×![]() ab,
ab,
即a2+2ab+b2=c2+2ab,
∴a2+b2=c2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目