Question

【题目】已知:点在上,弦,垂足,弦,垂足为,弦与相交于点；

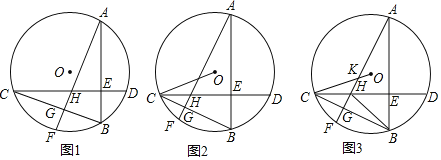
(1)如图,求证:；

(2)如图,连接,当平分时,求证:弧弧；

(3)如图,在(2)的条件下,半径与相交于点,连接,若,求线段的长.

Answer 1

【答案】(1)证明见解析；(2)证明见解析；(3)

【解析】

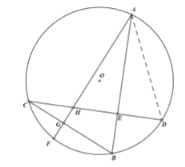
（1）连接AD,根据圆周角定理和垂线的性质可证明△AHD是等腰三角形，根据等腰三角形三线合一的性质即可证明；

（2）连接半径DO并延长DO交AF于点I，根据等腰三角形的性质和平行线的判定，可证明DI⊥AF，从而证明弧AD=弧FD；

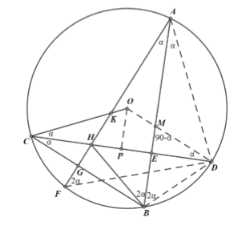
（3）连接DA，DF，DB，OD，DO与AB相交于点M，根据圆周角定理和垂线的性质可得BH=BD，再由三角函数值和三角形的面积求得CH和CD，然后过点O作OP⊥CD，垂足为点P，根据勾股定理和三角函数求出CG，进而求出CK.

(1)证明：连接

弧弧

（2）证明：连接半径并延长交于点

平分

弧弧

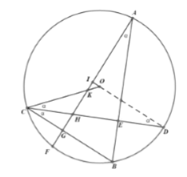
（3）证明：连接与相交于点

弧弧

由（1）（2）可知

设则

弧弧

是的垂直平分线

设则

在中则

或（舍）

过点作垂足为点