题目内容
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() (
(![]() 在左侧),与
在左侧),与![]() 轴交于点
轴交于点![]() ,若将它的图象向上平移4个单位长度,再向左平移5个单位长度,所得的抛物线的顶点坐标为
,若将它的图象向上平移4个单位长度,再向左平移5个单位长度,所得的抛物线的顶点坐标为![]() .
.
(1)原抛物线的函数解析式是 .
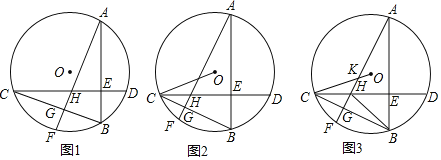
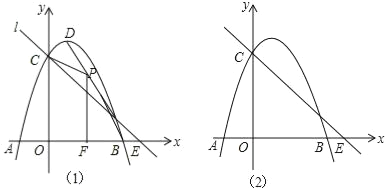
(2)如图①,点![]() 是线段
是线段![]() 下方的抛物线上的点,求
下方的抛物线上的点,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
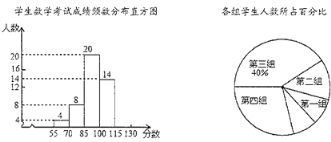
(3)如图②,点![]() 是线段
是线段![]() 上一动点,连接
上一动点,连接![]() ,在线段
,在线段![]() 上是否存在这样的点
上是否存在这样的点![]() ,使
,使![]() 为等腰三角形且
为等腰三角形且![]() 为直角三角形?若存在,求点
为直角三角形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)最大值
;(2)最大值![]() ,点P的坐标(
,点P的坐标(![]() ,
,![]() );(3)点M的坐标:(
);(3)点M的坐标:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)根据题意可推导出原抛物线的顶点坐标,然后再求出抛物线的解析式;
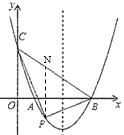
(2)过P作x轴的垂线交BC于N,则△PBC的面积分成△PNC和△PNB的面积之和,设出P的坐标,则△PBC的面积与P的坐标可建立函数关系式,进行求解即可;
(3)分类讨论并设出M的坐标,表示出MQ和MC的长,建立方程,求解即可.
解:(1)由题知,原抛物线的顶点坐标为(3,-4)
设原抛物线的解析式为![]()
则![]()
∴![]() 即
即![]()
(2)如图,过P作x轴的垂线交BC于N
令![]() ,则
,则![]()
∴![]() 即B(5,0),A(1,0)
即B(5,0),A(1,0)
令![]() ,则
,则![]()
∴C(0,5)
∴直线BC的解析式为![]()
设P(![]() ,
,![]() ),则N(
),则N(![]() ,
,![]() )
)
∴![]()
![]()
![]()
由二次函数性质可知:当![]() 时,
时,![]() 有最大值,且最大值为
有最大值,且最大值为![]()
此时P(![]() ,
,![]() )
)
(3)①如图所示,当∠BQM=90°时
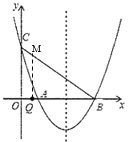
设Q(![]() ,0),则M(
,0),则M(![]() ,
,![]() )
)
则BQ=MQ=![]()
∴BM=![]()
又BC=![]()
∴CM=![]()
∵△CMQ为等腰三角形
∴![]() =
=![]()
解得:![]()
此时M(![]() ,
,![]() )
)
②如图所示:当∠BMQ=90°时
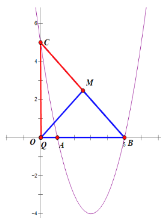
若△CMQ为等腰三角形,则△BMQ也为等腰三角形,则CM=BM=QM
此时M为BQ的中点
由(1)知:B(5,0),C(0,5)
∴M(![]() ,
,![]() )
)
综上所述,满足要求的点M的坐标为(![]() ,
,![]() )或M(
)或M(![]() ,
,![]() )
)

 阅读快车系列答案
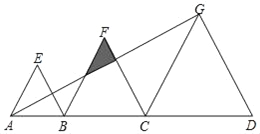
阅读快车系列答案【题目】如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则
①CD=____;
②图中阴影部分面积为_____.
【题目】根据扬州市某风景区的旅游信息,![]() 公司组织一批员工到该风景区旅游,支付给旅行社
公司组织一批员工到该风景区旅游,支付给旅行社![]() 元.
元. ![]() 公司参加这次旅游的员工有多少人?
公司参加这次旅游的员工有多少人?
扬州市某风景区旅游信息表
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加 |