题目内容
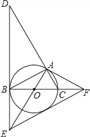
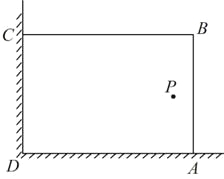
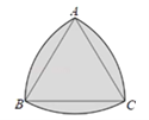
【题目】如图,四边形ABCD中,AB=AD,∠BAD=90°,∠BCD=30°,∠BAD的平分线AE与边DC相交于点E,连接BE、AC,若AC=7![]() ,△BCE的周长为16,则线段BC的长为____.
,△BCE的周长为16,则线段BC的长为____.
【答案】6
【解析】
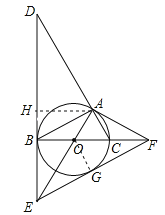
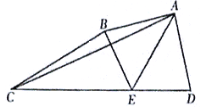
根据题意可先证明△ADE≌△ABE,得到DE=BE,然后分别作BF,AH垂直于CD交CD于点F、H,作AG垂直于FB并交FB的延长线于点G,证明四边形AGFH是正方形,再设BC=2x,在RT△BCF中,把三边都表示出来,根据勾股定理求x即可.
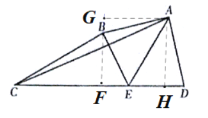
解:如图:
∵AE平分∠ BAD,
∴∠BAE=∠EAD,
又∵AB=AD,AE=AE,
∴△ADE≌△ABE,
∴DE=BE,
∵△BCE的周长为16,即BC+CE+BE=16,
∴BC+CE+DE=BC+CD=16,
分别作BF,AH垂直于CD交CD于点F、H,作AG垂直于FB并交FB的延长线于点G,
∴在四边形AGFH中,∠GAH=90°,
又∵∠BAD=90°,
∴∠GAB=∠DAH,
∵AB=AD,∠AGB=∠AHD=90°,
∴△ABG≌△ADH,
∴AG=AH,BG=HD,
∴四边形AGFH为正方形,
在RT△BCF中,∠BCD=30°,设BC=2x,则BF=x,CF=![]() x,CD=16-2x,
x,CD=16-2x,
∵CD=CF+FH+HD=16-2x,
∴CF+GF+HD=16-2x,
∴![]() x+x+BG+HD=16-2x,
x+x+BG+HD=16-2x,
∵BG=DH,
∴DH=![]() ,
,
∴CH=16-2x-![]() =
=![]() ,
,
∵AH=FG=BF+BG=x+![]() =
=![]() ,
,
在RT△ACH中,AC2=CH2+AH2,即(7![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,
)2,
解得x=3或x=5(根据线段长大于0舍去),所以BC=2x=6.
故本题答案为:6.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目