题目内容
【题目】如图,在□ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF

(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=8,CE=![]() ,求□ABCD的面积.
,求□ABCD的面积.
【答案】(1)证明见解析(2)36
【解析】试题分析:(1)根据平行四边形的性质和角平分线的性质得到四边形ABEF是平行四边形,然后再根据一组领边相等的平行四边形是菱形,证得结论;
(2)过点A作AH⊥BC于点H.根据菱形的对角线求出边长,然后根据面积的不变性求出平行四边形的高,从而求解.
试题解析:(1)证明:∵在□ABCD中,
∴AD∥BC.∴∠DAE=∠AEB.
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE.
∴四边形ABEF是菱形.
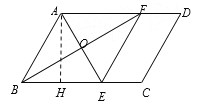
(2)解法一:过点A作AH⊥BC于点H.
∵四边形ABEF是菱形,AE=6,BF=8,
∴AE⊥BF,OE=3,OB=4.∴BE=5.
∵S菱形ABEF=![]() AEBF=BEAH,∴AH=
AEBF=BEAH,∴AH=![]() ×6×8÷5=
×6×8÷5=![]() .
.
∴S□ABCD=BCAH=(5+![]() )×
)×![]() =36.
=36.
解法二:∵四边形ABEF是菱形,AE=6,BF=8,
∴AE⊥BF,OE=3,OB=4.∴BE=5.
∵S菱形ABEF=![]() AEBF=
AEBF=![]() ×6×8=24,
×6×8=24,
∵CE=![]() ,BE=5,
,BE=5,
∴S□ABCD=![]() S菱形ABEF =
S菱形ABEF =![]() ×24=36.
×24=36.

练习册系列答案
相关题目