题目内容
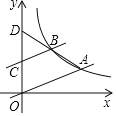
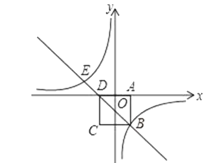
【题目】如图，在平面直角坐标系中，边长为 2 的正方形 ABCD 关于 y 轴对称，边 AD 在 x 轴上，点 B 在第四象限，直线 BD与反比例函数 y=
的图象交于 B、E 两点.
（1）求反比例函数的解析式；
（2）求点 E 的坐标
.
【答案】（1）
；（2）点E的坐标为（-2,1）.
【解析】
（1）根据正方形的边长，正方形关于y轴对称，可得点A、B、D的坐标，根据待定系数法，可得函数解析式；
（2）根据两个函数解析式，组成方程组，解方程组，即可得答案．
解：（1）∵边长为2的正方形ABCD关于y轴对称，边AD在x轴上，点B在第四象限，
∴A（1,0），D（-1,0），B（1，-2）.
∵反比例函数
的图象经过点B，
∴m=1
（-2）=-2.
∴反比例函数解析式为
.
（2）设直线BD的解析式为
，
∴
，
解得
.
∴直线BD的解析式为：
∵直线BD与反比例函数的图象交于B、E两点，
∴
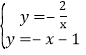
解得
或
∵B（1，-2）.
∴点E的坐标为（-2,1）.
练习册系列答案
阅读快车系列答案
相关题目
【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共4个，某学习小组进行摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再放回，下表是活动进行中的一组统计数据：
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 33 | 60 | 130 | 202 | 251 |
摸到黑球的频率 |
|
|
|
|
|
|
当n很大时，估计从袋中摸出一个黑球的概率是______；
试估算口袋中白球有______个；
在的条件下，若从中先换出一球，不放回，摇匀后再摸出一球，请用列表或树状图的方法求两次都摸到白球的概率．
