Question

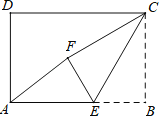
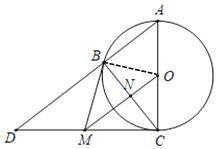
【题目】如图，⊙O是△ABC的外接圆，AC为直径，过C点作⊙O的切线，与AB延长线交于点D，M为CD的中点，连接BM，OM，且BC与OM相交于点N．

（1）求证：BM与⊙O相切；

（2）求证：2DM2＝BDOM；

（3）若sinA＝，BM＝3，求AB的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）5

【解析】

（1）连接OB，知∠OCB＝∠OBC，由直角三角形性质知BM＝CM＝DM，得∠MBC＝∠MCB，依据CD是⊙O的切线知∠OCB+∠DCB＝90°，据此可得∠OBC+∠MBC＝90°，可得结论；

（2）先证△DBC∽△DCA得，即CD2＝BDDA，再证OM是△ACD的中位线得AD＝2OE，两者结合即可得；

（3）由直角三角形的性质可得CD＝2BM＝6，即可求AD＝9，代入CD2＝ADBD，可求BD的长，即可求AB的长．

证明：（1）连接OB

∵OB＝OC

∴∠OBC＝∠OCB

∵AC是直径

∴∠ABC＝∠DBC＝90°

∵点M是CD中点，

∴BM＝CM＝DM

∴∠MBC＝∠MCB

∵CD是⊙O切线

∴∠ACD＝90°

∴∠OCB+∠MCB＝90°

∴∠OBC+∠MBC＝90°

即OB⊥BM，且OB是半径

∴BM是⊙O的切线

（2）∵AO＝CO，DM＝CM

∴AD＝2OM，AD∥OM

∵∠ACB+∠DCB＝90°，∠A+∠ACB＝90°

∴∠A＝∠DCB，且∠D＝∠D

∴△ACD∽△CBD

∴

∴CD2＝ADBD

∴（2DM）2＝2OMBD

∴2DM＝BDOM

（3）∵∠DBC＝90°，点M是CD的中点

∴CD＝2BM＝6

∵sinA＝＝，

∴AD＝9

∵CD2＝ADBD

∴BD＝4

∴AB＝AD﹣BD＝5