��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У���O��0��0������A����3��0������֪������y����x2+2mx+3��mΪ������������ΪP��
��1���������߾�����Aʱ������P������Ϊ�� ����
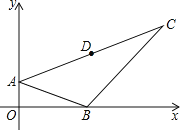
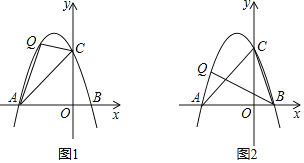
��2���ڣ�1���������£�����������x�����һ������Ϊ��B����y�ύ�ڵ�C����QΪֱ��AC�Ϸ���������һ���㣮
����ͼ1������QA��QC������QAC��������ֵ��
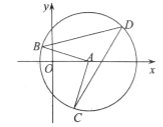
����ͼ2������CBQ��45�����������ʱ��Q���꣮
���𰸡���1������1��4������2����![]() ����Q����
����Q����![]() ��
��![]() ����
����
��������
��1������A������������߱���ʽ����ã�m=-1��������⣻
��2���ٹ���Q��y���ƽ���߽�AC�ڵ�N�������ֱ��AC�Ľ���ʽ����Q(x����x2��2x+3)�����N(x��x+3)�����QAC�����S=![]() ��QN��OA=��
��QN��OA=��![]() x2��
x2��![]() x��Ȼ����ݶ��κ��������ʼ�����⣻
x��Ȼ����ݶ��κ��������ʼ�����⣻
��tan��OCB=![]() ��
��![]() ����HM=BM=x����CM=3x��BC=BM+CM=4x=
����HM=BM=x����CM=3x��BC=BM+CM=4x=![]() ����ã�x=
����ã�x=![]() ��CH=
��CH=![]() x=
x=![]() �����H(0��
�����H(0��![]() )��ͬ���ɵã�ֱ��BH(Q)�ı���ʽΪ��y=-
)��ͬ���ɵã�ֱ��BH(Q)�ı���ʽΪ��y=-![]() x+
x+![]() ��������⣮
��������⣮
�⣺��1������A(��3��0)���������߱���ʽ����ã�
0����9-6m+3
��m����1��
�������ߵı���ʽΪ��y����x2��2x+3=-(x+1)2+4������
���P(��1��4)��
�ʴ�Ϊ��(��1��4)��
��2��������Q��y���ƽ���߽�AC�ڵ�N����ͼ1��
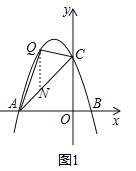
��ֱ��AC�Ľ���ʽΪy=kx+b��
����A(��3��0)��C(0��3)���������һ�κ�������ʽ����ã�
![]() ��
��
���
![]() ��
��
��ֱ��AC�ı���ʽΪ��y��x+3��
���Q(x����x2��2x+3)�����N��x��x+3����
��QAC�����S��![]() QN��OA��
QN��OA��![]() (��x2��2x+3��x��3)��3����
(��x2��2x+3��x��3)��3����![]() x2��
x2��![]() x��
x��
����![]() ��0����S�����ֵΪ��
��0����S�����ֵΪ��![]() ��
��
����ͼ2����ֱ��BQ��y���ڵ�H������H��HM��BC�ڵ�M��
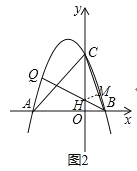
tan��OCB��![]() ��
��![]() ����HM��BM��x����CM��3x��
����HM��BM��x����CM��3x��
BC��BM+CM��4x��![]() ����ã�x��
����ã�x��![]() ��
��
CH��![]() x��
x��![]() �����H(0��
�����H(0��![]() )��
)��
ֱͬ��AC�ı���ʽ���ɵ�ֱ��BH��Q���ı���ʽΪ��y����![]() x+
x+![]() ������
������
�����٢�����ã�
��x2��2x+3=��![]() x+
x+![]() ��
��
���
x��1����ȥ����![]() ��
��
�ʵ�Q(��![]() ��
��![]() )��
)��

����Ŀ��������ó��˾����ij��ˮ���ɱ�Ϊ20Ԫ/![]() �������г����з��֣�����ˮ����δ��48������۵���
�������г����з��֣�����ˮ����δ��48������۵���![]() ��Ԫ/
��Ԫ/![]() ����ʱ��
����ʱ��![]() ���죩֮��ĺ�����ϵʽ
���죩֮��ĺ�����ϵʽ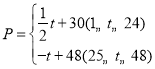 ��
��![]() ������������������
������������������![]() (
(![]() )��ʱ��
)��ʱ��![]() ���죩�Ĺ�ϵ���±���
���죩�Ĺ�ϵ���±���
ʱ�� | 1 | 3 | 6 | 10 | 20 | �� |
�������� | 118 | 114 | 108 | 100 | 80 | �� |
��1����֪![]() ��
��![]() ֮��ı仯����һ�κ�����ϵ�������ڵ�30�������������
֮��ı仯����һ�κ�����ϵ�������ڵ�30�������������
��2����һ���������������������������Ϊ���٣�
����Ŀ��С����![]() ,
,![]() ,
,![]() ,
,![]() �ĸ���С�ͳ��е�Ů������������ͳ�ƣ��������������ͳ��ͼ������֪
�ĸ���С�ͳ��е�Ů������������ͳ�ƣ��������������ͳ��ͼ������֪![]() ������Ů��20��.���г���Ů��ռ��ͳ�Ʊ�
������Ů��20��.���г���Ů��ռ��ͳ�Ʊ�
���� |
|
|
|
|
Ů������ռ�� | 62.5% | 62.5% | 50% | 75% |
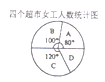
��1��![]() ���й���Ա�������ˣ�
���й���Ա�������ˣ�![]() ������Ů�������ˣ�
������Ů�������ˣ�
��2��������ЩŮ�������ѡ��һ������������![]() ���еĸ��ʣ�
���еĸ��ʣ�
��3������![]() �������н��С�ŮԱ����1�ˣ�
�������н��С�ŮԱ����1�ˣ�![]() ����Ů��ռ�Ȼ���75%�𣿼�ͬѧ��Ϊ�ǣ���ͬѧ��Ϊ����.����Ϊ˭˵�Ķԣ���˵������.
����Ů��ռ�Ȼ���75%�𣿼�ͬѧ��Ϊ�ǣ���ͬѧ��Ϊ����.����Ϊ˭˵�Ķԣ���˵������.