题目内容
【题目】已知直线AB:y=kx+b经过点B(1,4)、A(5,0)两点,且与直线y=2x-4交于点C.
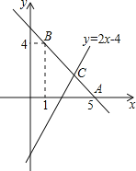
(1)求直线AB的解析式并求出点C的坐标;
(2)求出直线y=kx+b、直线y=2x-4及与y轴所围成的三角形面积;
(3)现有一点P在直线AB上,过点P作PQ∥y轴交直线y=2x-4于点Q,若线段PQ的长为3,求点P的坐标.
【答案】(1)y=-x+5;点C(3,2);(2)S=![]() ;(3)P点坐标为(2,3)或(4,1).
;(3)P点坐标为(2,3)或(4,1).
【解析】
(1)根据待定系数法求出直线AB解析式,再联立两函数解出C点坐标;
(2)依次求出y=-x+5和y=2x-4与y轴交点坐标,根据三角形的面积公式即可求解;
(3)设P点(m,-m+5) Q点坐标为(m,2m-4),根据线段PQ的长为3,分情况即可求解.
(1)∵直线y=kx+b经过点A(5,0),B(1,4),
∴ ![]()
解得 ![]()
∴直线AB的解析式为:y=-x+5;
∵若直线y=2x-4与直线AB相交于点C,
∴![]()
解得![]()
∴点C(3,2);
(2)∵y=-x+5与y轴交点坐标为(0,5),y=2x-4与y轴交点坐标为(0,-4)
,C点坐标为(3,2)
∴S=![]()
(3)设P点(m,-m+5) Q点坐标为(m,2m-4)
则-m+5-(2m-4)=3 或者2m-4-(-m+5)=3
解得m= 2 或m=4
∴P点坐标为(2,3)或(4,1).

 阅读快车系列答案
阅读快车系列答案【题目】甲、乙、丙三明射击队员在某次训练中的成绩如下表:
队员 | 成绩(单位:环) | |||||||||
甲 | 6 | 6 | 7 | 7 | 8 | 9 | 9 | 9 | 9 | 10 |
乙 | 6 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 10 |
丙 | 6 | 6 | 6 | 7 | 7 | 8 | 10 | 10 | 10 | 10 |
针对上述成绩,三位教练是这样评价的:
教练![]() :三名队员的水平相当;
:三名队员的水平相当;
教练![]() :三名队员每人都有自己的优势;
:三名队员每人都有自己的优势;
教练![]() :如果从不同的角度分析,教练
:如果从不同的角度分析,教练![]() 和
和![]() 说的都有道理.
说的都有道理.
你同意教练![]() 的观点吗?通过数据分析,说明你的理由.
的观点吗?通过数据分析,说明你的理由.
【题目】某公司欲招聘广告策划人员一名,对甲、乙、丙三名候选人进行三项素质测试,他们的各项测试成绩如下表所示:
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
创新 | 72 | 85 | 67 |
综合知识 | 50 | 74 | 70 |
语言 | 88 | 45 | 67 |
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按5:3:2的比例确定各人的测试成绩,此时谁将被录用?