题目内容
【题目】在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N
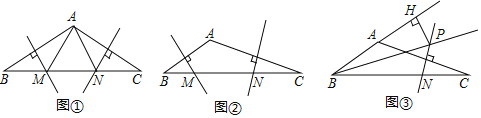
(1)如图①,若∠BAC=110°,则∠MAN= °,若△AMN的周长为9,则BC=
(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2;
(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=5,CB=12,求AH的长
【答案】(1)40;9;(2)见详解;(3)3.5
【解析】
(1)根据线段垂直平分线的性质得到AM=BM,NA=NC,根据等腰三角形的性质得到BAM=∠B,∠NAC=∠C,结合图形计算即可;
(2)连接AM、AN,仿照(1)的作法得到∠MAN=90°,根据勾股定理证明结论;
(3)连接AP、CP,过点P作PE⊥BC于点E,根据线段垂直平分线的性质得到AP=CP,根据角平分线的性质得到PH=PE,证明Rt△APH≌Rt△CPE得到AH=CE,证明△BPH≌△BPE,得到BH=BE,结合图形计算即可.
解:(1)∵∠BAC=110°,
∴∠B+∠C=180°﹣110°=70°,
∵AB边的垂直平分线交BC边于点M,
∴AM=BM,
∴∠BAM=∠B,
同理:NA=NC,
∴∠NAC=∠C,
∴∠MAN=110°﹣(∠BAM+∠NAC)=40°,
∵△AMN的周长为9,
∴MA+MN+NA=9,
∴BC=MB+MN+NC=MA+MN+NA=9,
故答案为:40;9;
(2)如图②,连接AM、AN,
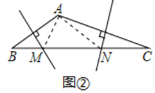
∵∠BAC=135°,
∴∠B+∠C=45°,
∵点M在AB的垂直平分线上,
∴AM=BM,
∴∠BAM=∠B,
同理AN=CN,∠CAN=∠C,
∴∠BAM+∠CAN=45°,
∴∠MAN=∠BAC﹣(∠BAM+∠CAN)=90°,
∴AM2+AN2=MN2,
∴BM2+CN2=MN2;
(3)如图③,连接AP、CP,过点P作PE⊥BC于点E,
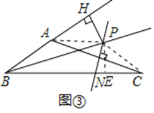
∵BP平分∠ABC,PH⊥BA,PE⊥BC,
∴PH=PE,
∵点P在AC的垂直平分线上,
∴AP=CP,
在Rt△APH和Rt△CPE中,
![]() ,
,
∴Rt△APH≌Rt△CPE(HL),
∴AH=CE,
在△BPH和△BPE中,
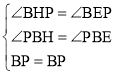 ,
,
∴△BPH≌△BPE(AAS)
∴BH=BE,
∴BC=BE+CE=BH+CE=AB+2AH,
∴AH=(BC﹣AB)÷2=3.5.

 阅读快车系列答案
阅读快车系列答案【题目】甲、乙、丙三明射击队员在某次训练中的成绩如下表:
队员 | 成绩(单位:环) | |||||||||
甲 | 6 | 6 | 7 | 7 | 8 | 9 | 9 | 9 | 9 | 10 |
乙 | 6 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 10 |
丙 | 6 | 6 | 6 | 7 | 7 | 8 | 10 | 10 | 10 | 10 |
针对上述成绩,三位教练是这样评价的:
教练![]() :三名队员的水平相当;
:三名队员的水平相当;
教练![]() :三名队员每人都有自己的优势;
:三名队员每人都有自己的优势;
教练![]() :如果从不同的角度分析,教练
:如果从不同的角度分析,教练![]() 和
和![]() 说的都有道理.
说的都有道理.
你同意教练![]() 的观点吗?通过数据分析,说明你的理由.
的观点吗?通过数据分析,说明你的理由.