题目内容
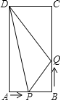
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 沿边
沿边![]() 从点
从点![]() 向点
向点![]() 以
以![]() 的速度移动;同时,点
的速度移动;同时,点![]() 从点
从点![]() 沿边
沿边![]() 向点
向点![]() 以
以![]() 的速度移动,设点
的速度移动,设点![]() 、
、![]() 移动的时间为
移动的时间为![]() .问:
.问:
![]() 当
当![]() 为何值时
为何值时![]() 的面积等于
的面积等于![]() ?
?
![]() 当
当![]() 为何值时
为何值时![]() 是直角三角形?
是直角三角形?
![]() 是否存在
是否存在![]() 的值,使
的值,使![]() 的面积最小,若存在,求此时
的面积最小,若存在,求此时![]() 的值及此时的面积;若不存在,请说明理由.
的值及此时的面积;若不存在,请说明理由.
【答案】(1)当![]() 或
或![]() 时,
时,![]() 的面积等于
的面积等于![]() ;(2)当
;(2)当![]() 的值为
的值为![]() 秒或
秒或![]() 秒或
秒或![]() 秒时,
秒时,![]() 是直角三角形;(3)存在,当
是直角三角形;(3)存在,当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
【解析】
(1)根据![]() ,
,![]() ,
,![]() ,△PBQ的面积等于8cm2,列出关于t的方程进行求解即可;
,△PBQ的面积等于8cm2,列出关于t的方程进行求解即可;
(2)根据∠PDQ<90°,需要分两种情况进行讨论:∠DPQ=90°或∠PQD=90°,分别求得t的值即可;
(3)根据AP=t,QB=2t,PB=6-t,可得S△DPQ=S梯形ABQD-S△APD-S△BPQ=![]() ,最后根据二次函数的性质,求得当t=3时,S△DPQ有最小值27.
,最后根据二次函数的性质,求得当t=3时,S△DPQ有最小值27.
解:![]() 由题意得
由题意得![]() ,
,![]() ,
,![]() .
.
∵![]() 的面积等于
的面积等于![]() ,
,
∴![]() ,
,
∴解得![]() 或
或![]() ,
,
又∵![]() ,
,
∴当![]() 或
或![]() 时,
时,![]() 的面积等于
的面积等于![]() .
.
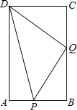
![]() 当
当![]() 时,点
时,点![]() ,
,![]() 分别与点
分别与点![]() ,
,![]() 重合,
重合,
此时,![]() ,
,![]() 是直角三角形;
是直角三角形;
当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
解得:![]() 或
或![]() ,
,
故当![]() 时,
时,![]() 是直角三角形;当
是直角三角形;当![]() 时,
时,![]() 点到达
点到达![]() 点、
点、![]() 点到达
点到达![]() 点,此时
点,此时![]() ,即
,即![]() 是直角三角形.
是直角三角形.
综上所述,当![]() 的值为
的值为![]() 秒或
秒或![]() 秒或
秒或![]() 秒时,
秒时,![]() 是直角三角形;
是直角三角形;
![]() 存在
存在![]() 的值,使
的值,使![]() 的面积最小.
的面积最小.
由题意得![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]() ,
,
![]() ,
,
![]() ,
,
又∵![]() ,
,
∴当![]() 时,
时,![]() 有最小值
有最小值![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某公司欲招聘广告策划人员一名,对甲、乙、丙三名候选人进行三项素质测试,他们的各项测试成绩如下表所示:
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
创新 | 72 | 85 | 67 |
综合知识 | 50 | 74 | 70 |
语言 | 88 | 45 | 67 |
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按5:3:2的比例确定各人的测试成绩,此时谁将被录用?