题目内容
如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里∕小时的速度向西北方向航行,我渔政船立即沿北偏东60º方向航行,1.5小时后,在我领海区域的C处截获可疑渔船。问我渔政船的航行路程是多少海里?(结果保留根号)
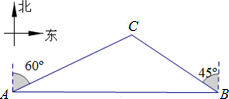

解:如图:作CD⊥AB于点D,

∵在Rt△BCD中,BC=12×1.5=18海里,∠CBD=45°,
∴CD=BC•sin45°=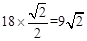 (海里)。
(海里)。
∴在Rt△ACD中,AC=CD÷sin30°=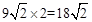 (海里)。
(海里)。
答:我渔政船的航行路程是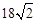 海里。
海里。

∵在Rt△BCD中,BC=12×1.5=18海里,∠CBD=45°,
∴CD=BC•sin45°=
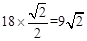 (海里)。
(海里)。∴在Rt△ACD中,AC=CD÷sin30°=
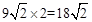 (海里)。
(海里)。答:我渔政船的航行路程是
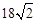 海里。
海里。解直角三角形的应用(方向角问题),锐角三角函数定义,特殊角的三角函数值。
【分析】过C点作AB的垂线,垂足为D,构建Rt△ACD,Rt△BCD,解这两个直角三角形即可。
【分析】过C点作AB的垂线,垂足为D,构建Rt△ACD,Rt△BCD,解这两个直角三角形即可。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
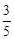 ,AB=4,则AC的长为多少?
,AB=4,则AC的长为多少? 

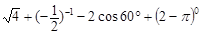 .
. 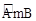 上的一点,则
上的一点,则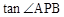 的值是【 】
的值是【 】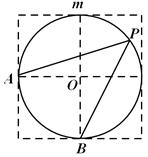
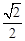 C.
C.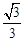 D.
D.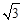
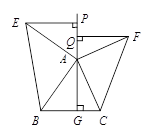
 ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分
ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分 ,EO=1,求∠EPF的度数;
,EO=1,求∠EPF的度数;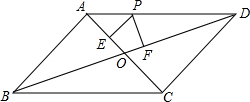
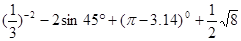 ..
..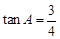 ,斜边AB=10,则直角边BC=_______.
,斜边AB=10,则直角边BC=_______.