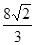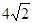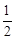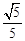题目内容
如图,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外侧作Rt△ABE和Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,
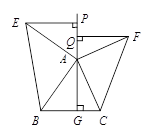
(1)若Rt△ABE和Rt△ACF都是等腰三角形,直接写出EP与FQ有怎样的数量关系;
(2)若Rt△ABE和Rt△ACF中满足AB=" k" AE,AC=" k" AF时,(1)中的结论还成立吗?若成立,请证明;若不成立,请探究EP与FQ有怎样的数量关系?
(3)若Rt△ABE和Rt△ACF中满足AB=" k" AE,AC= mAF时,联结EF交射线GA于点D,试探究ED与FD有怎样的数量关系?

(1)若Rt△ABE和Rt△ACF都是等腰三角形,直接写出EP与FQ有怎样的数量关系;
(2)若Rt△ABE和Rt△ACF中满足AB=" k" AE,AC=" k" AF时,(1)中的结论还成立吗?若成立,请证明;若不成立,请探究EP与FQ有怎样的数量关系?
(3)若Rt△ABE和Rt△ACF中满足AB=" k" AE,AC= mAF时,联结EF交射线GA于点D,试探究ED与FD有怎样的数量关系?
问题探究
(1)结论:EP=FQ.
(2)结论: EP=FQ.
理由:∵四边形ABME是矩形, ∴∠BAE=90°,∴∠BAG+∠EAP=90°.
∵AG⊥BC, ∴∠BAG+∠ABG=90°,∴∠ABG=∠EAP.
∵ ∠AGB=∠EPA=90° ∴ △ABG∽△EAP,
∴ = . ∵AB=" k" AE, ∴ = k
同理△ACG∽△FAQ,∴ = =" k"
= =" k"
∴ =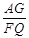 . ∴ EP=FQ.
. ∴ EP=FQ.
(3) .
.
由(2)可知:∴ = k, =m
∴ =" k," =" m." ∴
=" m." ∴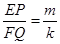
∵EP⊥GA,FQ⊥GA,∴ EP∥FQ.
∴
(1)结论:EP=FQ.
(2)结论: EP=FQ.
理由:∵四边形ABME是矩形, ∴∠BAE=90°,∴∠BAG+∠EAP=90°.
∵AG⊥BC, ∴∠BAG+∠ABG=90°,∴∠ABG=∠EAP.
∵ ∠AGB=∠EPA=90° ∴ △ABG∽△EAP,
∴ = . ∵AB=" k" AE, ∴ = k
同理△ACG∽△FAQ,∴
 = =" k"
= =" k" ∴ =
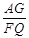 . ∴ EP=FQ.
. ∴ EP=FQ. (3)
 .
. 由(2)可知:∴ = k, =m
∴ =" k,"
 =" m." ∴
=" m." ∴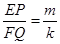
∵EP⊥GA,FQ⊥GA,∴ EP∥FQ.
∴

易证△AEP≌△BAG,△AFQ≌△CAG,即可求得EP=AG,FQ=AG,即可解题;
②易证△ABG∽△EAP,△ACG∽△FAQ,根据对应变成比例即可求解。
②易证△ABG∽△EAP,△ACG∽△FAQ,根据对应变成比例即可求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
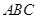 中,∠
中,∠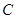 =90°,那么下列各式中,正确的是( )
=90°,那么下列各式中,正确的是( ) .
.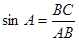 ;
; 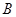 .
.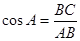 ;
; 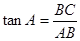 ;
; 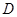 .
.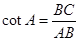 .
.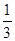 ,则sin∠A= ( )
,则sin∠A= ( )