Question

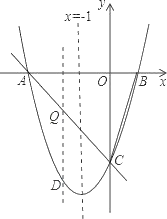
【题目】如图：对称轴x=﹣1的抛物线y=ax2+bx+c（a≠0）与x轴相交于A，B两点，其中点A的坐标为（﹣3，0），且点（2，5）在抛物线y=ax2+bx+c上．

（1）求抛物线的解析式．

（2）点C为抛物线与y轴的交点．

①点P在抛物线上，且S△POC=4S△BOC，求点P点坐标．

②设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．

Answer 1

【答案】（1）抛物线的解析式为：y=x2+2x﹣3；

（2）①点P的坐标为（4，21）或（﹣4，5）；

②当x=﹣时，QD有最大值．

【解析】试题分析：（1）因为抛物线的对称轴为x=-1，A点坐标为（-3，0）与（2，5）在抛物线上，代入抛物线的解析式，即可解答；（2）①先由二次函数的解析式为y=x2+2x-3，得到C点坐标，然后设P点坐标为（x，x2+2x-3），根据S△POC=4S△BOC列出关于x的方程，解方程求出x的值，进而得到点P的坐标；②先运用待定系数法求出直线AC的解析式为y=-x-3，再设Q点坐标为（x，-x-3），则D点坐标为（x，x2+2x-3），然后用含x的代数式表示QD，根据二次函数的性质即可求出线段QD长度的最大值．

试题解析：（1）因为抛物线的对称轴为x=﹣1，A点坐标为（﹣3，0）与（2，5）在抛物线上，则：

，

解得： ．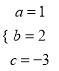

所以抛物线的解析式为：y=x2+2x﹣3．

（2）①二次函数的解析式为y=x2+2x﹣3，

∴抛物线与y轴的交点C的坐标为（0，﹣3），OC=3．

设P点坐标为（x，x2+2x﹣3），

∵S△POC=4S△BOC，

∴×3×|x|=4××3×1，

∴|x|=4，x=±4．当x=4时，x2+2x﹣3=16+8﹣3=21；

当x=﹣4时，x2+2x﹣3=16﹣8﹣3=5．

∴点P的坐标为（4，21）或（﹣4，5）；

②设直线AC的解析式为y=kx+t，将A（﹣3，0），C（0，﹣3）代入，

得，

解得： ．

即直线AC的解析式为y=﹣x﹣3．

设Q点坐标为（x，﹣x﹣3）（﹣3≤x≤0），则D点坐标为（x，x2+2x﹣3），

QD=（﹣x﹣3）﹣（x2+2x﹣3）=﹣x2﹣3x=﹣，

∴当x=﹣时，QD有最大值．