Question

【题目】如图，在ABCD中，DE=CE，连接AE并延长交BC的延长线于点F．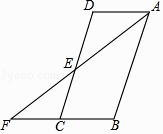

（1）求证：△ADE≌△FCE；
（2）若AB=2BC，∠F=36°．求∠B的度数．

Answer 1

【答案】
（1）

证明：∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC，

∴∠D=∠ECF，

在△ADE和△FCE中， ，

∴△ADE≌△FCE（ASA）

（2）

解：∵△ADE≌△FCE，

∴AD=FC，

∵AD=BC，AB=2BC，

∴AB=FB，

∴∠BAF=∠F=36°，

∴∠B=180°﹣2×36°=108°

【解析】（1）利用平行四边形的性质得出AD∥BC，AD=BC，证出∠D=∠ECF，由ASA即可证出△ADE≌△FCE；（2）证出AB=FB，由等腰三角形的性质和三角形内角和定理即可得出答案．
【考点精析】本题主要考查了平行四边形的性质的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能正确解答此题．