题目内容
【题目】求证：角平分线和中线重合的三角形是等腰三角形.
【答案】见解析
【解析】
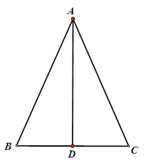
作出图形，延长AD到E，使DE=AD，连接BE，先证明△ADC和△EBD全等，根据全等三角形对应边相等得到AC=BE，对应角相等得到∠E=∠CAD，又中线也是角平分线，可以再证出AB=BE，从而证明AB=AC，所以是等腰三角形．
已知．在△ABC中，BD=CD，AD平分∠BAC．
求证：AB=AC．
证明：如图，延长AD到E，使DE=AD，连接BE．
∵AD是中线，∴BD=CD．在△ADC和△EBD中，∵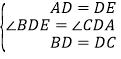
，∴△ADC≌△EBD（SAS），∴BE=AC，∠E=∠CAD．
∵AD是角平分线，∴∠CAD=∠BAD，∴∠E=∠BAD，∴AB=BE，∴AB=AC，∴△ABC是等腰三角形．
即：角平分线和中线重合的三角形是等腰三角形．
练习册系列答案
相关题目
