题目内容
【题目】如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
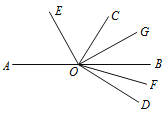
A. ∠DOG与∠BOE互补 B. ∠AOE-∠DOF=45°
C. ∠EOD与∠COG互补 D. ∠AOE与∠DOF互余
【答案】D
【解析】
根据角平分线的定义可设∠AOE=∠COE=α,∠BOG=∠COG=β,利用平角等于得出α+β=90°,∠EOG=90°.根据同角的余角相等得出∠DOG=∠COE=90°-∠COG=α,则∠BOD=∠DOG-∠BOG=α-β.∠BOF=∠DOF=![]() (α-β).然后根据互余、互补的定义分别判断即可.
(α-β).然后根据互余、互补的定义分别判断即可.
解:∵OE平分∠AOC,OG平分∠BOC,
∴可设∠AOE=∠COE=α,∠BOG=∠COG=β,
∵O为直线AB上一点,
∴∠AOB=180°,
∴2α+2β=180°,
∴α+β=90°,∠EOG=90°.
∵∠DOC=90°,
∴∠DOG=∠COE=90°-∠COG=α,
∴∠BOD=∠DOG-∠BOG=α-β.
∵OF平分∠BOD,
∴∠BOF=∠DOF=![]() (α-β).
(α-β).
A、∵∠DOG=α=∠AOE,∠AOE+∠BOE=180°,
∴∠DOG+∠BOE=180°,
故本选项结论正确,不符合题意;
B、∵∠AOE=α,∠DOF=![]() (α-β),
(α-β),
∴∠AOE-∠DOF=α-![]() (α-β)=
(α-β)=![]() (α+β)=45°,
(α+β)=45°,
故本选项结论正确,不符合题意;
C、∵∠EOD=∠EOG+∠GOD=90°+α,∠COG=β,
∴∠EOD+∠COG=90°+α+β=180°,
故本选项结论正确,不符合题意;
D、∵∠AOE+∠DOF=α+![]() (α-β)=
(α-β)=![]() α-
α-![]() β=
β=![]() α-
α-![]() (90°-α)=2α-45°,
(90°-α)=2α-45°,
∴当α=67.5°时,∠AOE+∠DOF=90°,
但是题目没有α=67.5°的条件,
故本选项结论错误,符合题意;
故选:D.